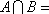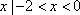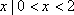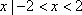- 复合函数的单调性
- 共281题
1
题型:简答题
|
定义域为







(1)判断函数

(2)如果函数


(3)对于区间







正确答案
见解析
解析
解析:(1)设





(2)若对于




……………………7分
若

若



综上所述得



假设当

那么,由
得

即
知识点
复合函数的单调性
1
题型:填空题
|
计算:
正确答案
2
解析
略
知识点
复合函数的单调性
1
题型:
单选题
|
若集合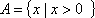
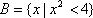
正确答案
B
解析
略
知识点
复合函数的单调性
1
题型:
单选题
|
“

正确答案
C
解析
略
知识点
复合函数的单调性
1
题型:
单选题
|
如图,某简单几何体的正(主)视图与侧(左)视图都是边长为1的正方形,且其体积为
正确答案
C
解析
略
知识点
复合函数的单调性
下一知识点 : 函数的最值
扫码查看完整答案与解析