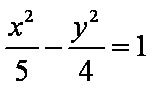
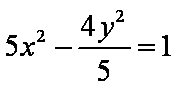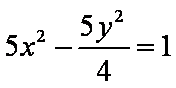- 复合函数的单调性
- 共281题
已知双曲线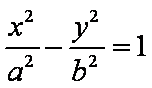
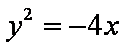
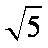
正确答案
解析
由题意得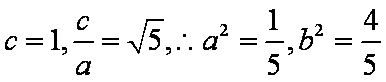
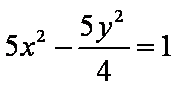
知识点
已知椭圆





(1)求椭圆
(2)若过点

正确答案
(1)
解析
解析:(1)

求得
所以椭圆方程为
(2)当斜率
当直线



所以

检验得

所以直线

知识点
设函数
(1)求函数

(2)是否存在非负实数


(3)定义

① 当

已知下面正确的命题:
当


② 若方程

正确答案
见解析
解析
解析: 函数
函数
(2)解:
则必须


(3)解:① 当

都有
② 由①可知

当
故有
因此同理归纳得到,当


要使方程

则必须
方程的根
这15个不同的实数根根的和.
知识点
已知变量




正确答案
9
解析
先根据约束条件画出变量








知识点
对于函数
(1)判断函数的单调性并证明;
(2)是否存在实数a使函数f (x)为奇函数?并说明理由。
正确答案
见解析。
解析
解:(1)函数f (x)的定义域是R
证明:设x1 < x2 ;
f (x1) – f (x2) = a

当



得f (x1) – f (x2) < 0所以f (x1) < f (x2)
故此时函数f (x)在R上是单调增函数;
当



得f (x1) – f (x2) 

故此时函数f (x)在R上是单调减函数
(2) f (x)的定义域是R,
由

当


满足条件

知识点
扫码查看完整答案与解析