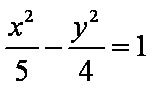
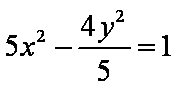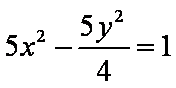- 复合函数的单调性
- 共281题
已知双曲线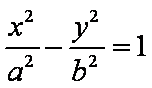
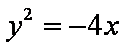
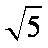
正确答案
解析
由题意得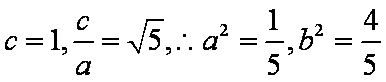
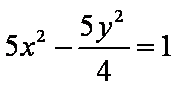
知识点
已知函数


(1)当


(2)当



(3)设函数








正确答案
见解析。
解析
函数

(1)当


若



若




当



当



所以函数


(2)当



当



当



所以函数


所以


又由



(3)由



若


解得
故

整理得,


令



设

当



当



所以,函数



知识点
已知椭圆





(1)求椭圆
(2)若过点

正确答案
(1)
解析
解析:(1)

求得
所以椭圆方程为
(2)当斜率
当直线



所以

检验得

所以直线

知识点
设函数
(1)求函数

(2)是否存在非负实数


(3)定义

① 当

已知下面正确的命题:
当


② 若方程

正确答案
见解析
解析
解析: 函数
函数
(2)解:
则必须


(3)解:① 当

都有
② 由①可知

当
故有
因此同理归纳得到,当


要使方程

则必须
方程的根
这15个不同的实数根根的和.
知识点
如图,两铁路线垂直相交于站A,若已知AB=100千米,甲火车从A站出发,沿AC方向以50千米/小时的速度行驶,同时乙火车从B站出发,沿BA方向以
(1)求甲、乙两车的最近距离(用含
(2)若甲、乙两车开始行驶到甲,乙两车相距最近时所用时间为


正确答案
见解析
解析
(1)设两车距离为



即两车的最近距离是

(2)当两车相距最近时,
此时
即当车速


知识点
已知变量




正确答案
9
解析
先根据约束条件画出变量








知识点
关于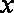
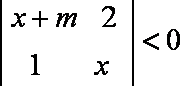
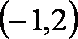
(1)求实数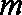
(2)若实系数一元二次方程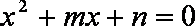

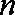
正确答案
见解析
解析
(1)原不等式等价于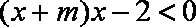
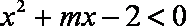
由题意得,解集为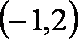
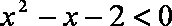
解得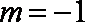
(2)由题意得:
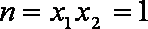
知识点
对于函数
(1)判断函数的单调性并证明;
(2)是否存在实数a使函数f (x)为奇函数?并说明理由。
正确答案
见解析。
解析
解:(1)函数f (x)的定义域是R
证明:设x1 < x2 ;
f (x1) – f (x2) = a

当



得f (x1) – f (x2) < 0所以f (x1) < f (x2)
故此时函数f (x)在R上是单调增函数;
当



得f (x1) – f (x2) 

故此时函数f (x)在R上是单调减函数
(2) f (x)的定义域是R,
由

当


满足条件

知识点
已知函数


(1)若

(2)设
① 当



② 设





正确答案
见解析。
解析
(1)当a=2,b=1时,
所以
令f ′(x)=0,得x1=-1,x2=
由表知f (x)的极大值是f (-1)=e-1,f (x)的极小值是f (
(2)① 因为g (x)=(ax-a)ex-f (x)=(ax-
当a=1时,g (x)=(x--2)ex。
因为g (x)≥1在x∈(0,+∞)上恒成立,
所以b≤x2-2x-
记h(x)=x2-2x-

当0<x<1时,h′(x)<0,h(x)在(0,1)上是减函数;
当x>1时,h′(x)>0,h(x)在(1,+∞)上是增函数。
所以h(x)min=h(1)=-1-e-1。
所以b的最大值为-1-e-1。
解法二:因为g (x)=(ax-a)ex-f (x)=(ax-
当a=1时,g (x)=(x-
因为g (x)≥1在x∈(0,+∞)上恒成立,
所以g(2)=

因为b<0,所以:当0<x<1时,g′(x)<0,g(x)在(0,1)上是减函数;
当x>1时,g′(x)>0,g(x)在(1,+∞)上是增函数。
所以g(x)min=g(1)=(-1-b)e-1
因为g (x)≥1在x∈(0,+∞)上恒成立,
所以(-1-b)e-1≥1,解得b≤-1-e-1
因此b的最大值为-1-e-1。
②解法一:因为g (x)=(ax-


由g (x)+g ′(x)=0,得(ax-


整理得2ax3-3ax2-2bx+b=0。
存在x>1,使g (x)+g ′(x)=0成立,
等价于存在x>1,2ax3-3ax2-2bx+b=0成立。
因为a>0,所以=。
设

因为x>1,u′(x)>0恒成立,所以u(x)在(1,+∞)是增函数,所以u(x)>u(1)=-1,
所以

解法二:因为g (x)=(ax-


由g (x)+g ′(x)=0,得(ax-

整理得2ax3-3ax2-2bx+b=0。
存在x>1,使g (x)+g ′(x)=0成立,
等价于存在x>1,2ax3-3ax2-2bx+b=0成立。
设u(x)=2ax3-3ax2-2bx+b(x≥1)
u′(x)=6ax2-6ax-2b=6ax(x-1)-2b≥-2b
当b≤0时,u′(x) ≥0
此时u(x)在[1,+∞)上单调递增,因此u(x)≥u(1)=-a-b
因为存在x>1,2ax3-3ax2-2bx+b=0成立
所以只要-a-b<0即可,此时-1<
当b>0时,
令
又u(1)=-a-b<0
于是u(x)=0,在(1,x0)上必有零点
即存在x>1,2ax3-3ax2-2bx+b=0成立,此时
综上有
知识点
已知

(1)当


(2)求函数

正确答案
见解析
解析
(1)由题意,
当


当


综上,所求解集为
(2)①当



∵
∴
∴
② 当


③当









∴综上,
知识点
扫码查看完整答案与解析