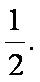- 复合函数的单调性
- 共281题
函数y=ex﹣lnx的值域为 。
正确答案
[2,+∞)
解析
定义域为(0,+∞),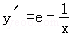
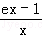
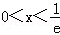
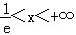
所以函数在区间(0,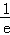
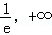
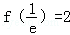
知识点
已知函数f(x)=
(1)求y=f(x)在点P(0,1)处的切线方程;
(2)设g(x)=f(x)+x-1仅有一个零点,求实数m的值;
(3)试探究函数f(x)是否存在单调递减区间?若有,设其单调区间为[t,s],试求s-t的取值范围?若没有,请说明理由。
正确答案
见解析。
解析
(1)∵点P在函数y=f(x)上,由f(x)=

(2)由g(x)=f(x)+x-1=

则
①当m=1时,

②当m>1时,则
又∵x→-1时,g(x)→-

故此种情况不符题意。………………………………9分
(3)假设y=f(x)存在单调区间,由f(x) =

令


即, 


知识点
如图,在平面直角坐标系




(1)若过点




(2)设动圆


①证明:动圆圆心C在一条定直线上运动;
②动圆
坐标;若不经过,请说明理由。
正确答案
见解析
解析
解:(1)设直线


因为直线



所以圆心



化简,得


所以直线


(2)①证明:设圆心

即
化简得
即动圆圆心C在定直线
②圆

则动圆C的半径为
于是动圆C的方程为
整理,得
由

所以定点的坐标为

知识点
各项均为正偶数的数列a1,a2,a3,a4中,前三项依次成公差为d(d > 0)的等差数列,后三项依次成公比为q的等比数列. 若
正确答案
解析
解析一:
设四个数为:
∴


所以四个数为:



由题意

又


∴

当



当


当


解析二:设这四个数为







所以

所以
当


当

当


所以q的所有可能值构成的集合为
知识点
如图,在平面直角坐标系





(1)求直线
(2)求直线


(3)是否存在分别以
正确答案
见解析
解析
解: (1)因为

所以直线BD的方程为
(2)线段BP的垂直平分线方程为x=0,线段AP的垂直平分线方程为
所以圆C的圆心为(0,-1),且圆C的半径为
又圆心(0,-1)到直线BD的距离为


为
(3)假设存在这样的两个圆M与圆N,其中PB是圆M的弦,PA是圆N的弦,则点M一定在y轴上,点N一定在线段PC的垂直平分线


设



解得
所以

知识点
已知a,b为常数,a≠0,函数
(1)若a=2,b=1,求f(x)在(0,+∞)内的极值;
(2)①若a>0,b>0,求证:f(x)在区间[1,2]上是增函数;
②若f(2)<0,f(﹣2)<e﹣2,且f(x)在区间[1,2]上是增函数,求由所有点(a,b)形成的平面区域的面积。
正确答案
见解析。
解析
(1)若a=2,b=1,则f(x)=(2+
则f′(x)=(x+1)(2x﹣1)
由f′(x)>0,得x>
由f′(x)<0,得0<x<
则当x=


(2)f′(x)=(ax2+bx﹣b)
设g(x)=ax2+bx﹣b,
①证明:若a>0,b>0,则二次函数g(x)的图象开口向上,对称轴x=﹣
∴g(x)>0,对一切x∈[1,2]恒成立,
又
②若f(2)<0,f(﹣2)<e﹣2,
则

∵f(x)在区间[1,2]上是增函数,
∴f′(x)≥0对x∈[1,2]恒成立,即
在(•),(••)的条件下,b<0,且1<
且g(

综上求由所有点(a,b)满足的约束条件为
则不等式组对应的平面区域为△OAB,其中A(

则形成的平面区域的面积S=S△OAC﹣S△OBC=
即△OAB的面积为
知识点
已知A(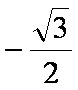
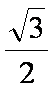
(1)求动点P的轨迹方程;
(2)设直线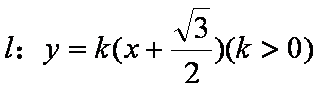
正确答案
见解析。
解析
(1)∵|PA|+|PB|=2>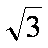
∴点P的轨迹是以A,B为焦点,长轴长2a=2的椭圆,…………………………………………2分
∴a=1, 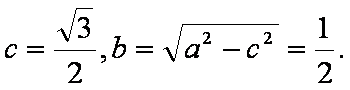
设P(x,y),∴点P的轨迹方程为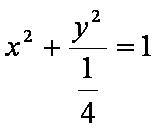
(2)将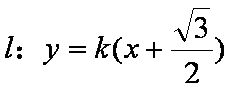
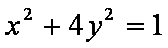
消去x,整理为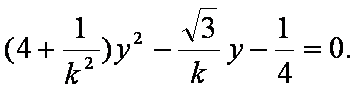
设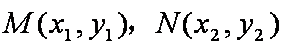
则
=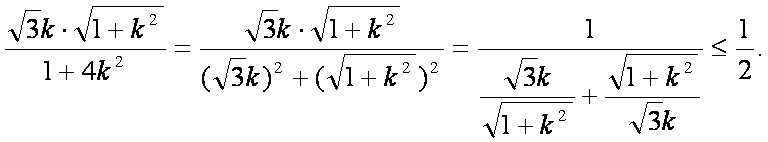
当且仅当
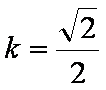
此时直线l的方程是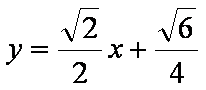
知识点
定义:

正确答案
解析
易得


知识点
设函数f(x)满足f(x)=f(3x),且当x∈[1,3)时,f(x)=lnx,若在区间[1,9)内,存在3个不同的实数x1,x2,x3,使得




正确答案
(

解析
设x∈[3,9),则
∵x∈[1,3),f(x)=lnx,
∴f(

∵函数f(x)满足f(x)=f(3x),
∴f(x)=
∵在区间[1,9)内,存在3个不同的实数x1,x2,x3,使得


∴f(x)﹣tx=0在区间[1,9)上有三个解,
则y=t与h(x)=
当x∈[1,3),h(x)=


∴当x∈[1,e)时,h′(x)>0,
当x∈(e,3)时,h′(x)<0即函数h(x)=
∴当x=e处,函数h(x)=

当x∈[3,9),h(x)=


∴当x∈[3,3e)时,h′(x)>0,当x∈(3e,9)时,h′(x)<0,
即函数h(x)=
∴当x=3e处,函数h(x)=

根据函数的单调性,以及h(1)=0,h(e)=


根据图象可知y=t与h(x)在[1,3)上一个交点,在[3,3e) 上两个交点,
∴在区间[1,9)内,函数g(x)=f(x)﹣tx有三个不同零点,则实数a的取值范围是(

知识点
已知等差数列




(1)求

(2)令



正确答案
见解析
解析
(1)设等差数列




所以



(2)由(1),知
所以bn=


所以


知识点
扫码查看完整答案与解析