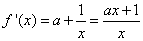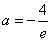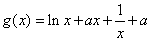· 函数的基本性质

· 复合函数的单调性

复合函数的单调性
共281题

· 函数的基本性质

· 复合函数的单调性

复合函数的单调性
共281题

热门试卷

X 查看更多试卷

1

题型：单选题

|

单选题 · 5 分

从中任取一个数x，从中任取一个数y，则使的概率为

A

B

C

D

正确答案

A

解析

如图，使是图中阴影部分，故所求的概率

.

知识点

复合函数的单调性

1

题型：简答题

|

简答题 · 12 分

在锐角△ABC中，a、b、c分别为角A，B，C所对的边，且.

（1）求角C的大小；

（2）若，且的面积为，求的值.

正确答案

见解析

解析

知识点

复合函数的单调性

1

题型：单选题

|

单选题 · 5 分

某三棱锥的三视图如图2所示，则该三棱锥的体积是（）

A

B

C

D

正确答案

B

解析

略

知识点

复合函数的单调性

1

题型：简答题

|

简答题 · 14 分

已知函数f（x）＝ax＋lnx（a＜0）

（1）若当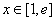时，函数f（x）的最大值为－3，求a的值；

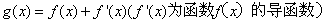
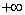
（2）设，若函数g（x）在（0，）上是单调函数，求a的取值范围。

正确答案

见解析。

解析

（1）由

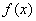
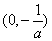
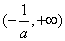
可得函数在上单调递增，在上单调递减，

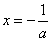
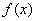
∴当时，取最大值

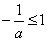
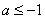
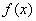
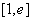
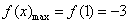
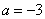
①当，即时，函数在上单调递减，

∴，解得；

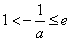
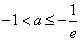
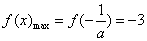
②当，即时，，

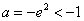
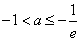
解得，与矛盾，不合舍去；

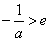
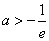
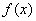
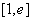
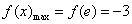
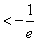
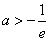
③当，即时，函数在上单调递增，

∴，解得，与矛盾，不合舍去；

综上得。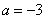

（2）解法一：∵，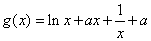

∴，

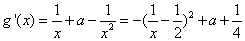
显然，对于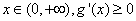不可能恒成立，

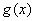
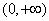
∴函数在上不是单调递增函数，

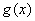
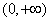
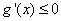
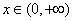
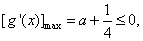
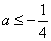
若函数在上是单调递减函数，则对于恒成立，

∴解得，

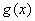
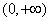
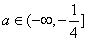
综上得若函数在上是单调函数，则。

【解法二：∵

∴，

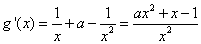
令------------（）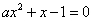

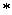
方程（）的根判别式，

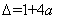
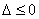
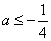
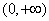
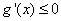
当，即时，在上恒有，

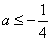
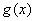
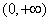
即当时，函数在上是单调递减；

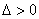
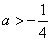
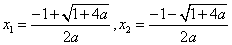
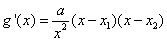
当，即时，方程（）有两个不相等的实数根：

；

∴，

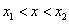
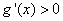
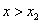
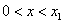
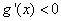
当时，当或时，，

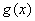
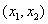
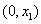
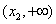
即函数在单调递增，在或上单调递减，

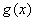
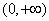
∴函数在上不单调，

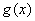
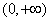
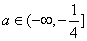
综上得若函数在上是单调函数，则。

知识点

复合函数的单调性

1

题型：填空题

|

填空题 · 5 分

已知直线（为参数且）与曲线(是参数且)，则直线与曲线的交点坐标为　　　 .

正确答案

（1，3）

解析

把直线的参数方程化为普通方程得，把曲线的参数方程化为普通方程得，由方程组解得交点坐标为（1，3）

知识点

复合函数的单调性

继续学习学习下一知识点

下一知识点 : 函数的最值

百度题库 > 高考 > 文科数学 > 复合函数的单调性

扫码查看完整答案与解析