- 复合函数的单调性
- 共281题
设p:实数x满足



(1)若

(2)若p是q的必要不充分条件,求实数
正确答案
见解析
解析
(1)由

当




由




若


所以实数

(2) p是q的必要不充分条件,即q

设A=


又




所以当

当

所以实数

知识点
已知圆











(1)讨论曲线

(2)当













正确答案
见解析
解析
(1)连结



此时
故



当


故


――――4分
(2)当




联立方程
设


∴



同理,直线

∵|AT|·|TC|=|BT|·|TD| ∴
又



又直线


知识点
已知函数
(1)当


(2)讨论函数
正确答案
见解析。
解析
(1)当

∴
∵



∴


而
∴
(2)
①当



②当


③当



∴


综上,
当


当



当


知识点
已知函数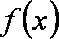
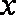
(1)已知函数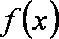
(2)若函数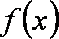
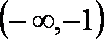
(3)试证明对
正确答案
见解析。
解析
(1)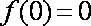
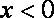
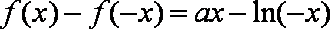
所以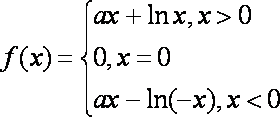
(2)函数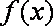
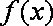
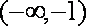
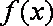
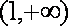
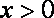
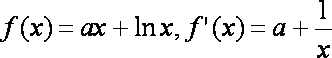
由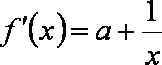
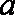
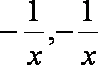
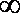
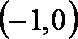
所以a的取值范围为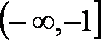
(3)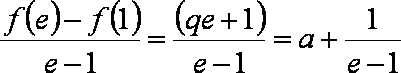

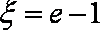
知识点
命题甲: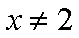
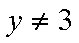
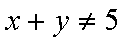
正确答案
解析
甲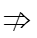
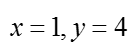
乙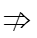
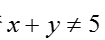
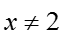
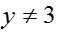
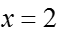
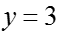
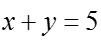
知识点
扫码查看完整答案与解析