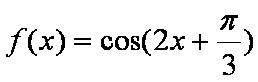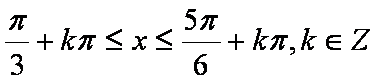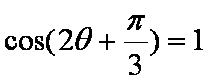- 复合函数的单调性
- 共281题
设函数



(1)若

(2)当



正确答案
见解析
解析
(1)由题意得

即


∴
∴
令
令
令
∴


∴

(2)当


等价于

令

因
故当



∴


当


∵


故当
∴

综上可得
知识点
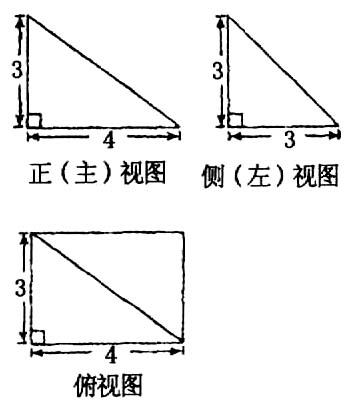
一个棱锥的三视图如图所示,则这个棱锥的体积为 ▲
.
正确答案
12
解析
由三视图可知,这是一个底面为矩形,两侧面和底面垂直的四棱锥,底面矩形长4宽为3,四棱锥的高为3,所以四棱锥的体积为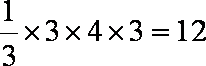
知识点
在面积为S的矩形ABCD内随机取一点P,则

正确答案
解析

由图象可知当点P在矩形的中线EF上移动时,






知识点
过点A(2,3)且垂直于直线
正确答案
解析
法一:设所求直线方程为



法二:直线





知识点
已知向量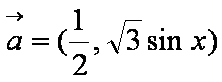
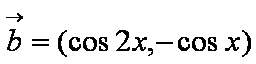
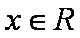
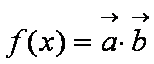
(1)求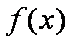
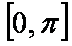
(2)若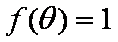
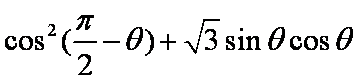
正确答案
见解析
解析
(1)
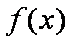
由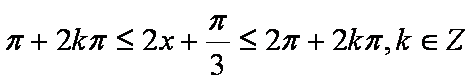
又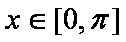
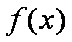
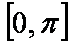
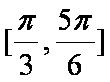
(2)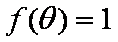
∴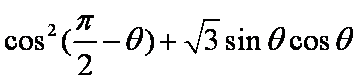
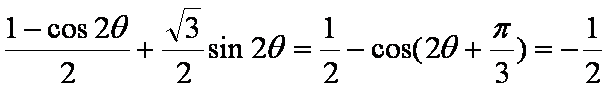
知识点
扫码查看完整答案与解析