- 复合函数的单调性
- 共281题
命题甲: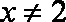
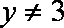
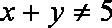
正确答案
解析
甲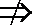
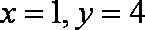
乙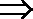
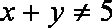
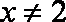
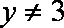
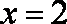
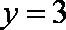
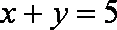
此逆否命题为真命题,所以原命题为真命题。
知识点
某工厂为扩大生产规模,今年年初新购置了一条高性能的生产线,该生产线在使用过程中的维护费用会逐年增加,第1年的维护费用是4万元,从第2年到第7年,每年的维护费用均比上年增加2万元,从第8年开始,每年的维护费用比上年增加25%。
(1)设第n年该生产线的维护费用为an,求an的表达式;
(2)设该生产线前n年的维护费用为Sn,求Sn.
正确答案
见解析
解析
(1)由题意知,当n≤7时,数列{an}是首项为4,公差为2的等差数列,
故an=4+(n-1)×2=2n+2. …………………..2分
当n≥8时,数列{an}从a7开始构成首项为a7=2×7+2=16,公比为1+25%=的等比数列,
则此时an=16×n-7,……………………………5分
所以an=..................6分
(2)当1≤n≤7时,Sn=4n+×2=n2+3n,……………..8分
当n≥8时,由S7=70,得Sn=70+16××=80×n-7-10,
……………………..10分
所以该生产线前n年的维护费用为
Sn=...............13分
知识点
山东省《体育高考方案》于2012年2月份公布,方案要求以学校为单位进行体育测试,某校对高三1班同学按照高考测试项目按百分制进行了预备测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.
(1) 请估计一下这组数据的平均数M;
(2) 现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成一个小组.若选出的两人成绩差大于20,则称这两人为“帮扶组”,试求选出的两人为“帮扶组”的概率.
正确答案
见解析。
解析
(1) 由频率分布直方图可知:50~60分的频率为0.1,60~70分的频率为0.25,
70~80分的频率为0.45,80~90分的频率为0.15,90~100分的频率为0.05;…………………………………………………………………… 2分
∴这组数据的平均数M=55×0.1+65×0.25+75×0.45+85×0.15+95×0.05=73(分)
…………………………………………………………………………………4分
(2) ∵90~100分数段的人数为2人,频率为0.05;
∴参加测试的总人数为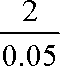
∴50~60分数段的人数为40×0.1=4人,………………………………… 6分
设第一组50~60分数段的同学为A1,A2,A3,A4;第五组90~100分数段的同学为B1,B2…………………………………………………………………… 7分
则从中选出两人的选法有:
(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2),共15种;……
…………………………………………………………………………………9分
其中两人成绩差大于20的选法有:(A1,B1),(A1,B2),(A2,B1),(A2,B2),
(A3,B1),(A3,B2),(A4,B1),(A4,B2)共8种……………………………………… 11分
则选出的两人为“帮扶组”的概率为P=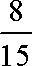
知识点
设函数f(x)=lnx,g(x)=ax+
(1)求a、b的值;
(2)设x>0,试比较f(x)与g(x)的大小。
正确答案
见解析。
解析
(1)∵
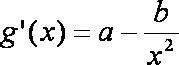
∴由题意可得: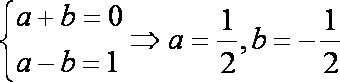
(2)由(1)可知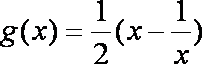
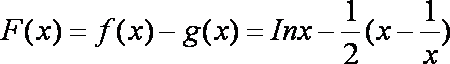
∵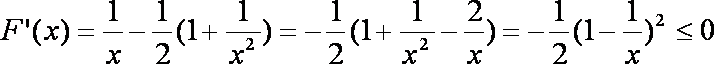
∴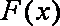
∴当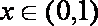
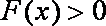
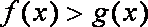
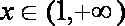
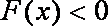
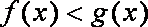
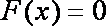
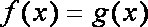
知识点
设平面向量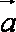
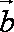
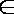
(1)记“使得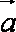
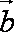
(2)记“使得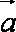
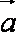
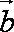
正确答案
见解析。
解析
(1)有序数组(m,n)的所有可能结果为:(-2,-2),(-2,-1),(-2,1),(-2,2),
(-1,-2),(-1,-1),(-1,1),(-1,2),(1,-2),(1,-1),(1,1),(1,2),(2,-2),
(2,-1),(2,1),(2,2)共有16种. ……………………………………………………3分
使得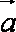
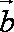
事件A有(-1,2), (1,-2)有2种。 ……………………………………………5分
故所求的概率为: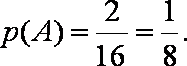
(2)使得
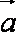
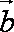
m(1-2n)-(m-4)=0即: mn=-2 …………………………………………………9分
事件B有: (-2,1),(-1,2),(1,-2),(2,-1)4种 ……………………………11分
故所求的概率为: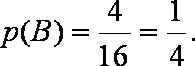
知识点
扫码查看完整答案与解析