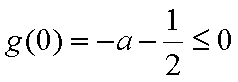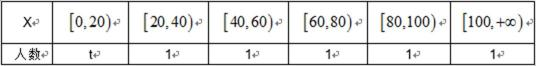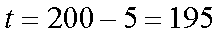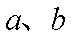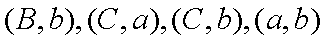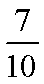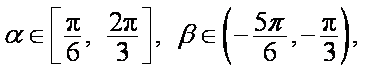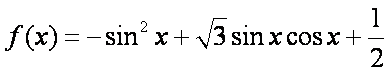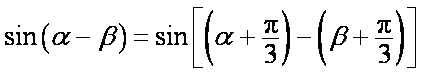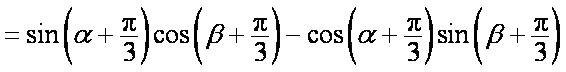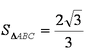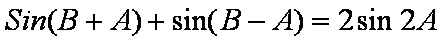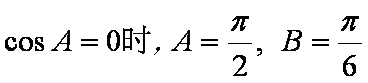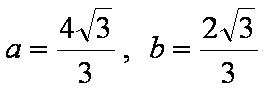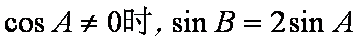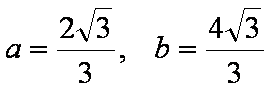- 复合函数的单调性
- 共281题
已知函数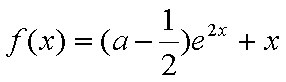
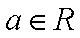
(1)若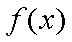
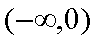
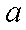
(2)若在区间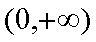
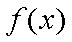
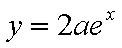
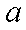
正确答案
见解析。
解析
(1)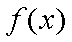
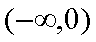
则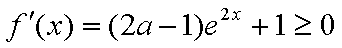
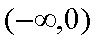
即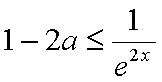
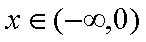
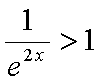
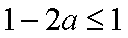
所以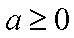
(2)令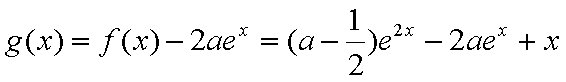
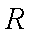
在区间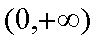
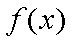
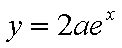
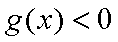
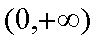
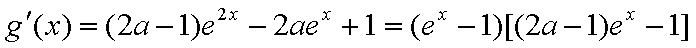
① 若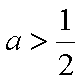
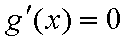
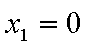
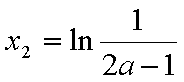
当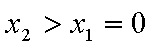
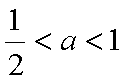
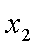
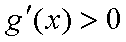
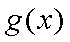
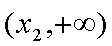
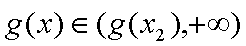
当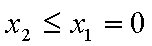
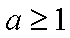
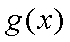
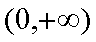
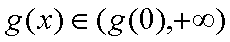
也不合题意;
② 若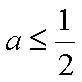
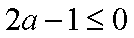
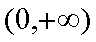
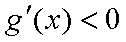
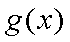
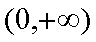
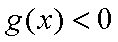
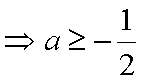
由此求得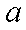
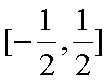
综合①②可知,当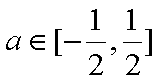
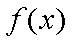
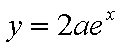
知识点
设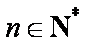
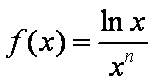
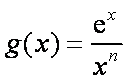
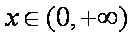
(1)判断函数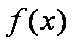
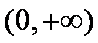
(2)若当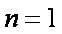
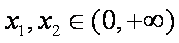
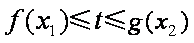
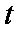
(3
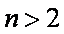

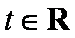
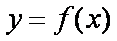
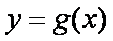
正确答案
见解析
解析
解析:
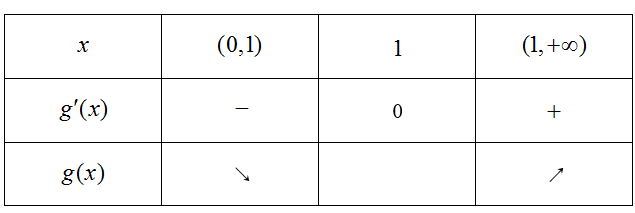
(1)解:结论:函数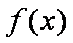
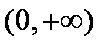
求导,得 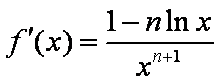
令 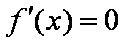
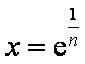
当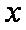
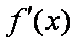
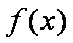
所以函数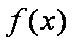
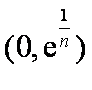
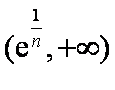
所以函数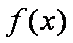
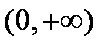

(2)解:当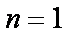
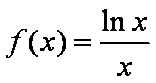
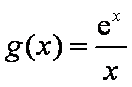
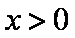
由题意,若对任意的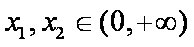
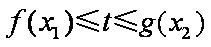
只需当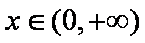
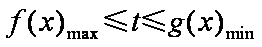
因为 
令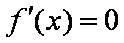
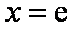
当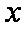
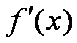
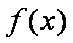
所以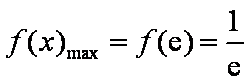
又因为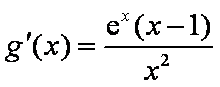
令 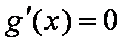
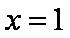
当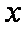
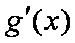
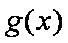
所以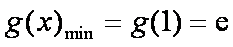
综上所述,得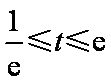
(3)解:满足条件的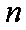
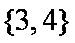
知识点
公安部交管局修改后的酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其判断标准是驾驶人员每100毫升血液中的酒精含量X毫克,当20≤X<80时,认定为酒后驾车;当X≥80时,认定为醉酒驾车,重庆市公安局交通管理部门在对G42高速路我市路段的一次随机拦查行动中,依法检测了200辆机动车驾驶员的每100毫升血液中的酒精含量,酒精含量X(单位:毫克)的统计结果如下表:。
依据上述材料回答下列问题:
(1)求t的值:
(2)从酒后违法驾车的司机中随机抽取2人,求这2人中含有醉酒驾车司机的概率
正确答案
见解析。
解析
(1)
(2)令酒后驾车的司机分别为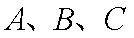
抽取的可能为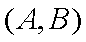
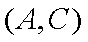
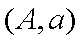
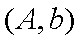
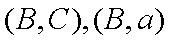
则含有醉酒驾车司机概率为
知识点
已知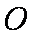
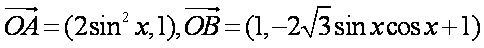
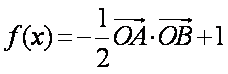
(1)求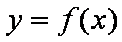
(2)将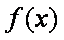

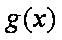
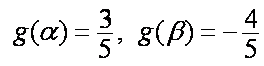
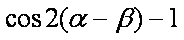
正确答案
见解析。
解析
(1)由题设有,
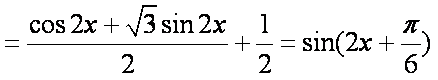
∴函数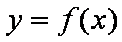
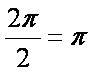
(2)由题设有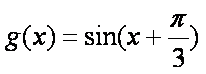
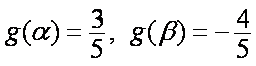
即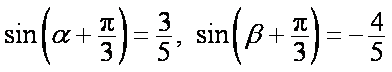
因为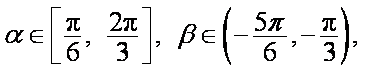
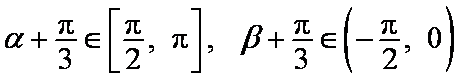
∴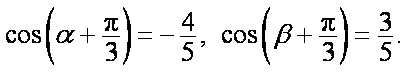
∴
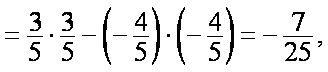
所以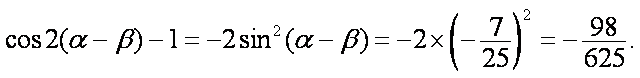
知识点
已知函数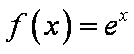
(1)当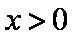
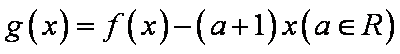
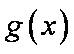
(2)证明当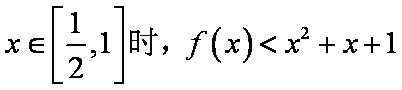
正确答案
见解析。
解析
(1)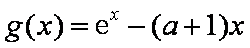
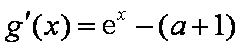
当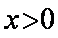
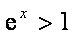
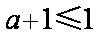
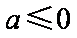
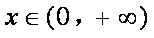
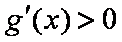
当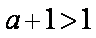
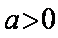
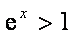
令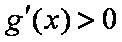
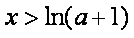
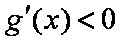
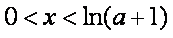
综上,当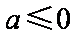
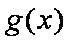
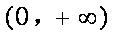
当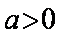
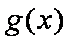
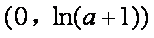
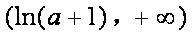
(2)设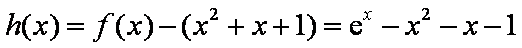
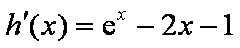
令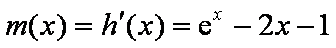
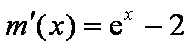
因为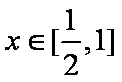

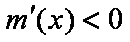
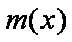
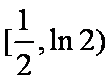
当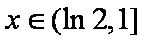
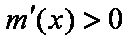
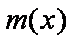
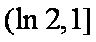
又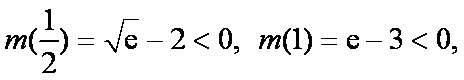
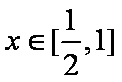
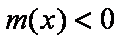
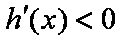
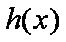

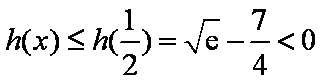
即当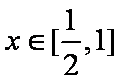
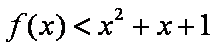
知识点
在△ABC中,内角A、B、C对边的边长分别是a、b、c,已知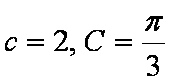
(1)若△ABC的面积等于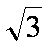
(2)若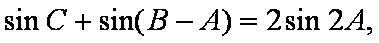
正确答案
(1)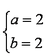
解析
解析:(1)由余弦定理及已知条件得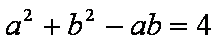
又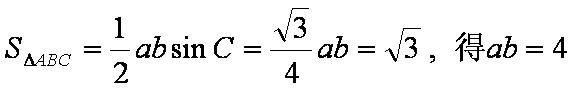
①②联立解得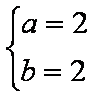
(2)由题设得
即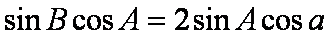
当
根据正弦定理,得
此时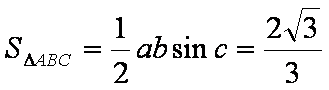
当
由正弦定理,得 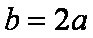
联立①与③解得
此时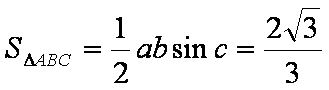
综合,得
知识点
下列函数中,既是偶函数,又在区间[-1,0]上是减函数的是
正确答案
解析
函数y=cosx的图象关于y轴对称,是偶函数,但在区间[-1,0]上为增函数,故A不满足要求;
函数y=log2x既不是偶函数,也不是奇函数,故C不满足要求;
函数y=ex—e-x 中,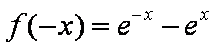
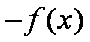
故答案为:B。
知识点
已知数列




(1)求数列
(2) 若点








正确答案
见解析。
解析
(1)由



当

所以
(2)由

综上所述当


知识点
在锐角

(1)求角B的大小及角A的取值范围;
(2)设

正确答案
见解析。
解析
(1)由正弦定理得
所以
即
因为

因为
又因


(2)
=-2(



所以

知识点
设
正确答案
解析

故
知识点
扫码查看完整答案与解析