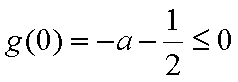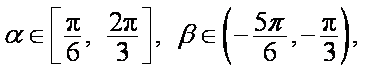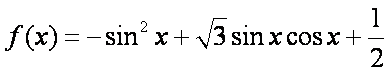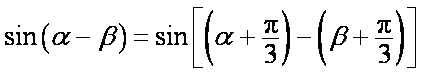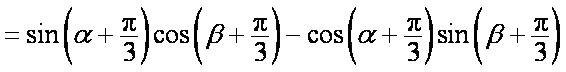- 复合函数的单调性
- 共281题
已知函数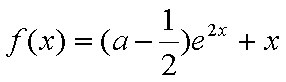
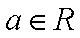
(1)若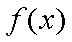
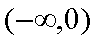
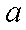
(2)若在区间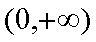
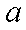
正确答案
见解析。
解析
(1)
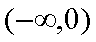
则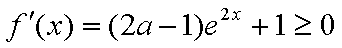
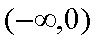
即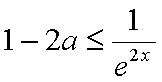
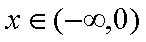
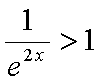
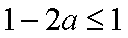
所以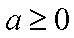
(2)令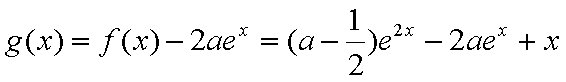
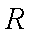
在区间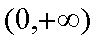
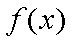
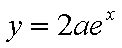
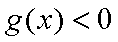
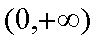
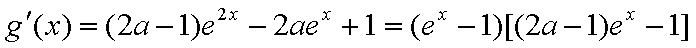
① 若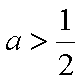
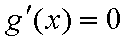
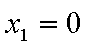
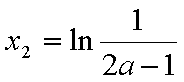
当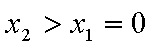
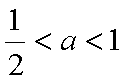
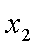
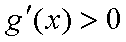
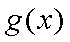
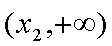
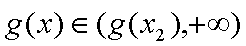
当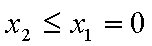
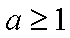
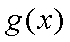
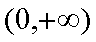
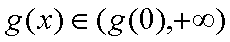
也不合题意;
② 若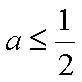
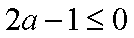
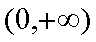
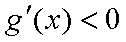
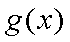
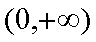
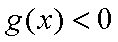
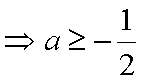
由此求得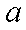
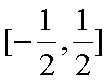
综合①②可知,当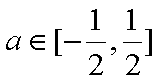
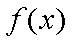
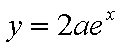
知识点
设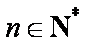
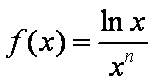
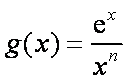
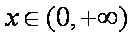
(1)判断函数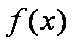
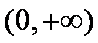
(2)若当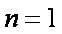
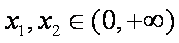
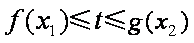
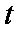
(3
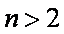

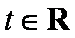
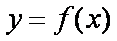
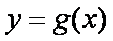
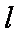
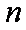
正确答案
见解析
解析
解析:
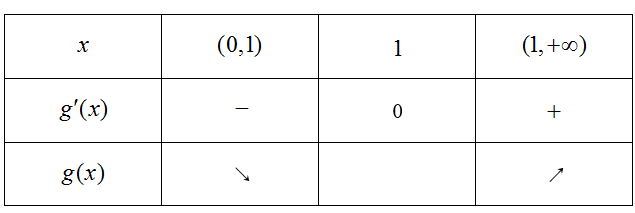
(1)解:结论:函数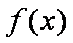
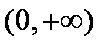
求导,得 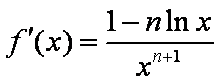
令 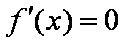
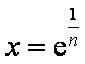
当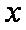
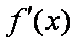
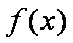
所以函数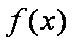
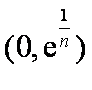
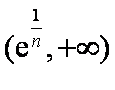
所以函数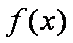
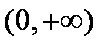

(2)解:当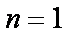
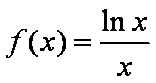
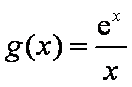
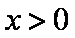
由题意,若对任意的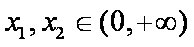
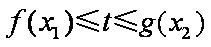
只需当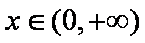
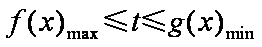
因为 
令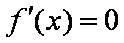
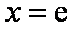
当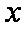
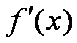
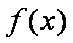
所以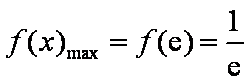
又因为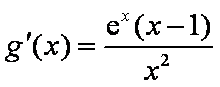
令 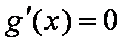
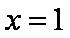
当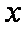
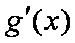
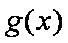
所以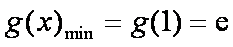
综上所述,得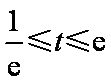
(3)解:满足条件的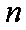
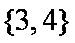
知识点
已知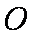
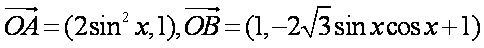
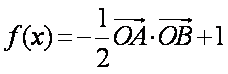
(1)求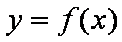
(2)将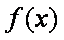

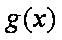
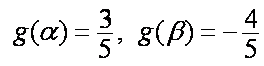
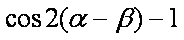
正确答案
见解析。
解析
(1)由题设有,
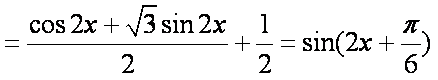
∴函数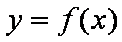
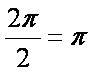
(2)由题设有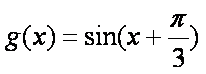
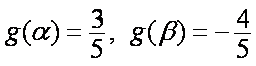
即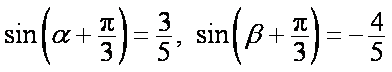
因为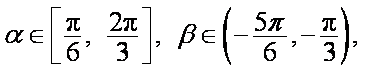
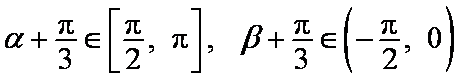
∴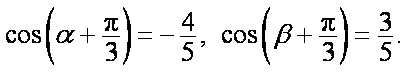
∴
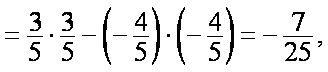
所以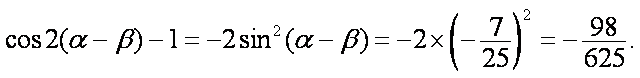
知识点
已知数列




(1)求数列
(2) 若点








正确答案
见解析。
解析
(1)由



当

所以
(2)由

综上所述当


知识点
在锐角

(1)求角B的大小及角A的取值范围;
(2)设

正确答案
见解析。
解析
(1)由正弦定理得
所以
即
因为

因为
又因


(2)
=-2(



所以

知识点
扫码查看完整答案与解析