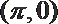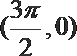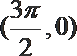- 三角恒等变换
- 共635题
17.空气污染,又称为
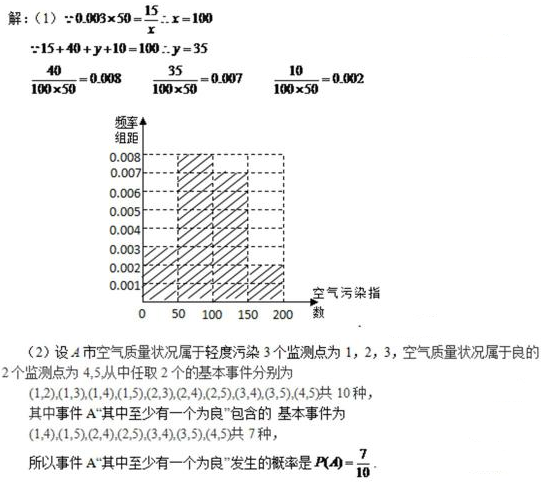
(1)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
(2)若A市共有5个监测点,其中有3个监测点为轻度污染,2个监测点为良.从中任意选取2个监测点,事件A“其中至少有一个为良”发生的概率是多少?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.如图,游客从某旅游景区的景点






















(Ⅰ)求索道
(Ⅱ)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(Ⅲ)为使两位游客在

正确答案
(Ⅱ)由(Ⅰ)知: 


所以由余弦定理得,
即

所以


故


∴为使两位游客在


解法二:(Ⅰ)如图作BD⊥CA于点D,
设BD=20k,则DC=25k,AD=48k,AB=52k
由AC=63k=1260m,知:AB=52k=1040m.
(Ⅱ)设乙出发x分钟后到达点M,
此时甲到达N点,如图所示.
则:AM=130x,AN=50(x+2),
由余弦定理得:MN2=AM2+AN2-2 AM·ANcosA=7400 x2-14000 x+10000,
其中0≤x≤8,当x=
此时乙在缆车上与甲的距离最短.
解析
解析已在路上飞奔,马上就到!
知识点
14.下列命题正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知关于


(1)当

(2)若

正确答案
(1)

解之,得 
(2)







则 

综上,得 
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数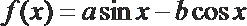
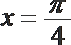
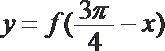
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知函数
(Ⅰ)求函数

(Ⅱ)若对于任意的


正确答案
(Ⅰ)

∵


∴


(Ⅱ)∵对于任意的

∴


解得

解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求函数f(x)的表达式;
(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在


(I) 求
(II) 求
正确答案
(Ⅰ)解:在△ABC中,根据正弦定理,
(Ⅱ)解:在△ABC中,根据余弦定理,得cosA=
于是 sinA=

所以 sin(2A-


解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数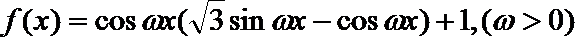
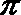
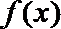
正确答案
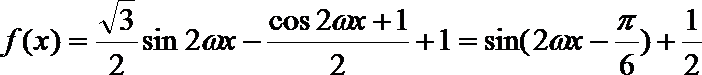
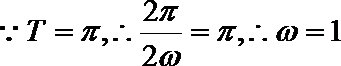
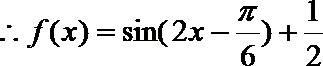
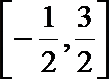
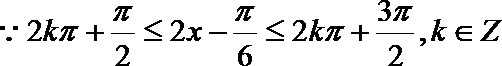
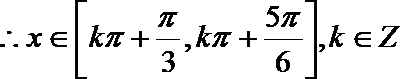
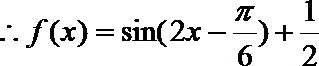
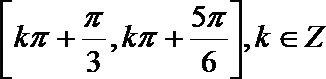
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析