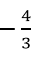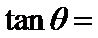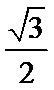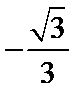- 三角恒等变换
- 共635题
14.已知θ是第四象限角,且sin(θ+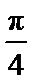
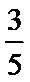

正确答案
知识点
4.若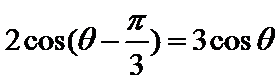
正确答案
解析
由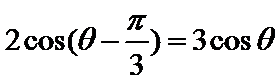
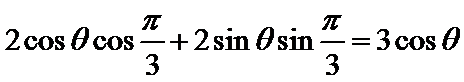
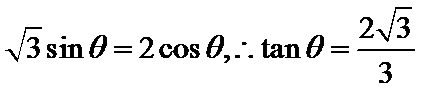
考查方向
解题思路
先根据两角差的余弦公式将题中给出的等式化简为关于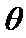
易错点
不会利用两角差的余弦公式展开题中给出的条件,对于的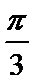
知识点
已知函数
(1)求函数
(2)若

正确答案
(1)f(x)的最小正周期为2
(2)
解析
(1)由已知,f(x)=
所以f(x)的最小正周期为2

(2)由(1)知,f(
所以cos(
所以

知识点
已知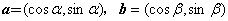
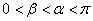
(1)若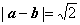
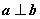
(2)设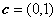
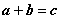
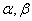
正确答案
见解析
解析
(1)a-b=(cosα-cosβ,sinα-sinβ),
|a-b|2=(cosα-cosβ)2+(sinα-sinβ)2=2-2(cosα·cosβ+sinα·sinβ)=2,
所以,cosα·cosβ+sinα·sinβ=0,
所以,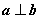
(2)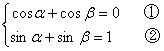
所以,α-β=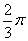
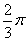
带入②得:sin(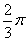
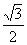
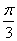
所以,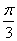
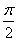
所以,α=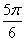
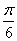
知识点
函数f(x)=sin(x+φ)﹣2sinφcosx的最大值为 1 。
正确答案
1
解析
∵f(x)=sin(x+φ)﹣2sinφcosx=sinxcosφ+cosxsinφ﹣2sinφcosx=sinxcosφ﹣sinφcosx=sin(x﹣φ)。
∴f(x)的最大值为1
知识点
已知函数

(1)求
(2)已知



正确答案
见解析
解析
(1)




(2)证明:由已知得
两式相加得



∴
知识点
设0<θ<




正确答案
解析
∵

∴2sinθ﹣cosθ=0,∴tanθ=
知识点
已知函数
(1)求f(x)的单调递增区间;
(2)若α是第二象限角,
正确答案
(1)函数f(x)的单调递增区间为
(2)cos α-sin α=
解析
(1)因为函数y=sin x的单调递增区间为
由

所以,函数f(x)的单调递增区间为
(2)由已知,有
即sin α+cos α=
当sin α+cos α=0时,由α是第二象限角,知
此时,
当sin α+cos α≠0时,有(cos α-sin α)2=
由α是第二象限角,知cos α-sin α<0,
此时cos α-sin α=
综上所述,cos α-sin α=

知识点
9.化简:4sin40°-tan40°等于( )
正确答案
解析
试题分析:本题属于三角函数中的基本问题,题目的难度是逐渐由易到难。注意化简时对两角和差公式的选取.
考查方向
本题主要考查了三角函数的公式化简计算,在近几年的各省高考题出现的频率较高,常与三角恒等变形公式等知识点交汇命题。
解题思路
本题考查三角函数的公式化简计算,解题步骤如下:
由题可知,函数解析式化简为(2sin80°-sin40°)/cos40°=[2cos(40°-30°)-sin40°]/cos40°=

易错点
本题易在公式化简上发生错误。
知识点
14.已知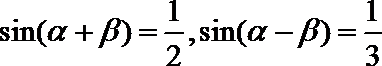

正确答案
1
解析
由题可知,将展开的两式相加减,可求出tana/tanb=5,代入对数式得值为1.
考查方向
本题主要考查了两角和差公式及对数运算
解题思路
本题考查两角和差公式及对数运算,解题思路如下:利用两角和差公式展开已知,两式相加减,求出正切值;代入对数式求解。
易错点
本题必须注意两角和差公式
知识点
扫码查看完整答案与解析