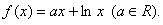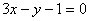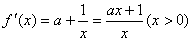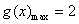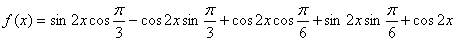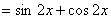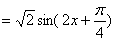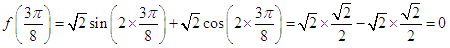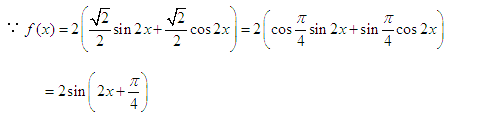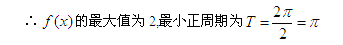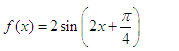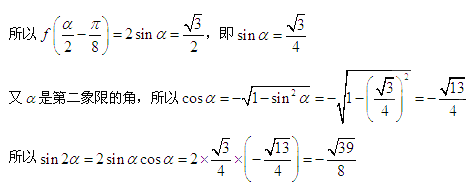- 三角恒等变换
- 共635题
已知函数
(1)若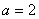
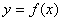
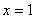
(2)求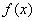
(3)设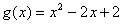
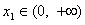
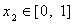
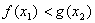
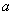
正确答案
见解析。
解析
(1)由已知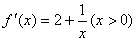
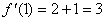
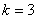
又切点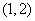
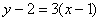
故曲线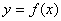
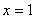
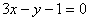
(2)
①当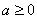
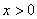
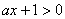
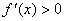
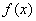
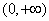
②当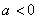
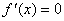
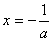
在区间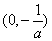
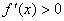
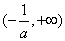
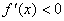
所以,函数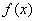
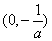
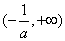
(3)由已知,转化为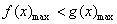

由(2)知,当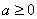
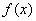
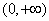
(或者举出反例:存在
当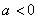
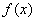
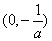
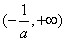
故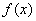
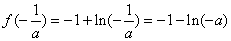
所以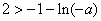
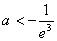
知识点
已知函数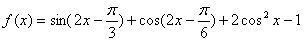
(1)求函数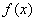
(2)求函数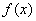
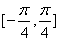
正确答案
见解析。
解析
(1)
所以函数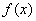
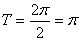
(2)因为
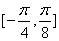

又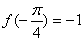
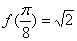
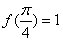
故函数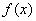
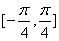
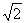
知识点
函数
正确答案
解析
略
知识点
函数
正确答案
解析



知识点
设函数f(x)=sinxcosx-cos(x+π)cosx(x∈R)。
(1)求f(x)的最小正周期;
(2)若函数y=f(x)的图象按b=平移后得到函数y=g(x)的图象,求y=g(x)在上的最大值。
正确答案
见解析。
解析
知识点
已知函数
(1)求函数
(2)在



求

正确答案
(1)
解析
(1)∵
∴
由

∴函数

(2)∵在

∴

又
∴
依据正弦定理,有
∴
∴
知识点
设函数



(1)求
(2)在






正确答案
见解析。
解析
(1)


令
解得
故
注:若没写
(2)由
而


又
知识点
已知函数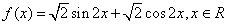
(1)求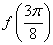
(2)求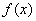
(3)若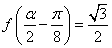
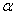
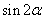
正确答案
见解析。
解析
(1)
(2)
(3)
由(2)可知
知识点
已知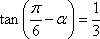
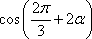
正确答案
解析
设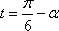
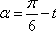
则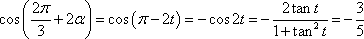
知识点
正确答案
见解析。
解析
知识点
扫码查看完整答案与解析