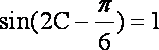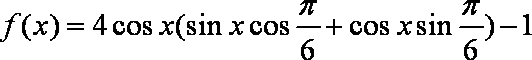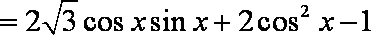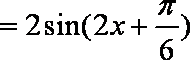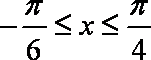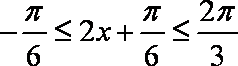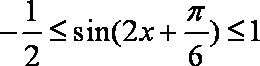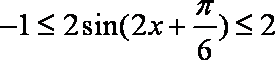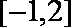- 三角恒等变换
- 共635题
已知函数
(1)求函数

(2)求函数
正确答案
见解析。
解析
(1)


(注:此处也可是
所以
此时

(2)因为余弦函数的增区间为

∴
∴
∴

知识点
已知函数

(1)求函数
(2)若函数




正确答案
见解析。
解析
(1)



当

函数

(2)函数





即


知识点
已知函数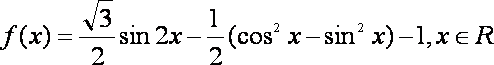
(1)求函数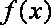
(2)设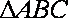
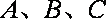
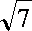
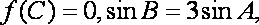

正确答案
见解析。
解析
(1)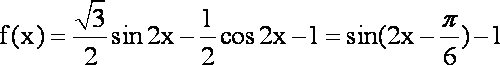

(2)由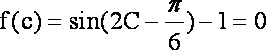
又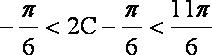
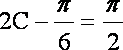
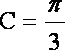
由余弦定理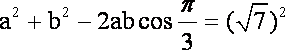
由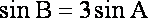
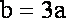
由①②得,a=1,b=3………………………………………………………………………12分
知识点
已知


(1)求角
(2)若
正确答案
见解析。
解析
(1)∵




∵


(2)由题知
∴

∴

而


知识点
已知数列


(1)求数列

(2)记
正确答案
见解析。
解析
(1)当

当

又
∴
(2)∵
当
∴

知识点
在
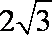
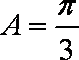
(1)若b=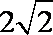
(2)若c=2,求边b的长。
正确答案
(1)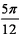
解析
解析:(1)由正弦定理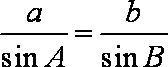
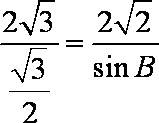
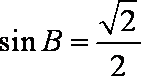
由于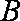
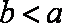
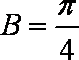
所以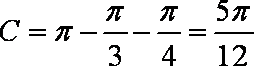
(2)依题意,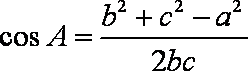
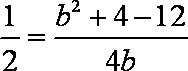
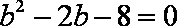
又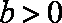
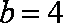
另解:
由于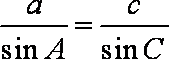
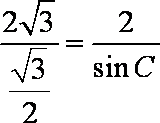
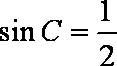
由于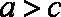
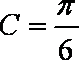
由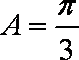
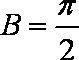
由勾股定理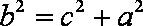
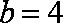
知识点
已知函数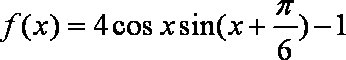
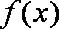
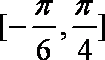
正确答案
见解析。
解析
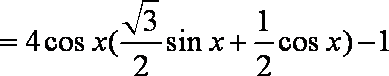
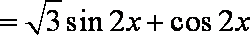
∵
∴
∴
所以,函数在区间的值域是
知识点
若函数


(1)求

(2)若点



正确答案
见解析。
解析
(1)
由题意知,



函数



(2)





因此点

知识点
设
(1)求函数
(2)当
正确答案
见解析。
解析
(1)

所以函数的单调递增区间是
(2)

知识点
已知
(1)求
(2)当
正确答案
见解析。
解析
(1)

所以
令

故所求对称中心的坐标为
(2)

即

知识点
扫码查看完整答案与解析