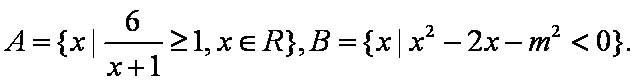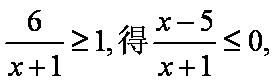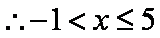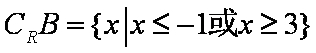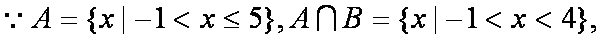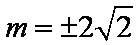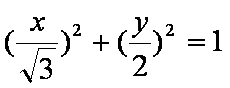- 诱导公式的推导
- 共79题
在△ABC中,sin2C=

正确答案
解析
由正弦定理知
所以

知识点
已知单调递增的等比数列{



(1)求数列{an}的通项公式。
(2)若



正确答案
见解析。
解析
(1)设等比数列

依题意,有

∴



又


(2)
∴
∴ 
∴①-②得
=
知识点
某单位设计的两种密封玻璃窗如图所示:图1是单层玻璃,厚度为8 mm;图2是双层中空玻璃,
厚度均为4 mm,中间留有厚度为

两侧的温度差为


假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等,(注:玻璃的热传导系
数为

(1)设室内,室外温度均分别为



且
的热量(结果用


(2)为使双层中空玻璃单位时间内,在单位面积上通过的热量只有单层玻璃的4%,应如何设计
正确答案
见解析。
解析
(1)设单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量分别为

则

(2)由(1)知
当

答:当
知识点
已知集合
(1)当
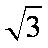
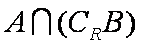
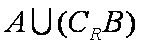
(2)若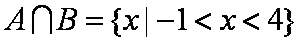
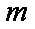
正确答案
见解析
解析
解析:由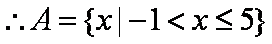
(1)当m=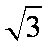
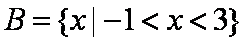
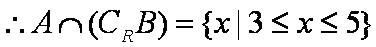
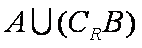
(2)
则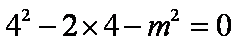
此时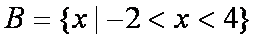
知识点
设函数

正确答案
解析
∵函数f(x)=ex(sinx-cosx),∴f′(x)=(ex)′(sinx-cosx)+ex(sinx-cosx)′=2exsinx,
∵x∈(2kπ,2kπ+π)时,f′(x)>0,x∈(2kπ+π,2kπ+2π)时,f′(x)<0,
∴x∈(2kπ,2kπ+π)时原函数递增,x∈(2kπ+π,2kπ+2π)时,函数f(x)=ex(sinx-cosx)递减,故当x=2kπ+π时,f(x)取极大值,其极大值为f(2kπ+π)=e2kπ+π[sin(2kπ+π)-cos(2kπ+π)]=e2kπ+π×(0-(-1))=e2kπ+π,又0≤x≤2012π,∴函数f(x)的各极大值之和S=eπ+e3π+e5π+…+e2011π=
知识点
在平面直角坐标系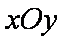
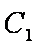
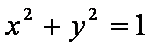
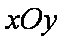
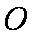
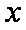

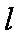
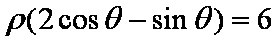
(1)将曲线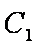
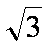
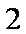
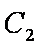
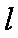
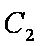
(2)在曲线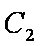
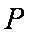
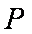
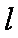
正确答案
见解析
解析
(1)由题意知,直线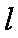
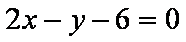
由题意知曲线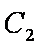
∴曲线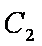
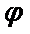
(2)设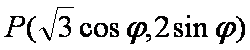

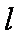
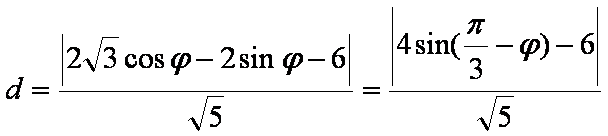
当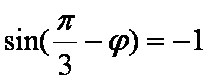
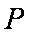
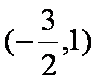
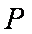
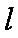
此时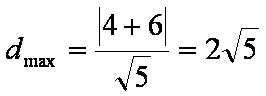
知识点
设






正确答案
解析
略
知识点
提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度





(1)当

(2)当车流密度

正确答案
见解析。
解析
(1)由题意当



2分
显然


解得
故函数


(2)依题意并由(1)可得
当



当

当且仅当

所以,当



综上,当



即当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时。12分
知识点
若函数


正确答案
解析
略
知识点
在




(1)求角B;
(2)若

正确答案
见解析
解析
(1)




(2)

由正弦定理:

知识点
扫码查看完整答案与解析