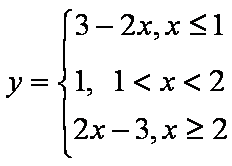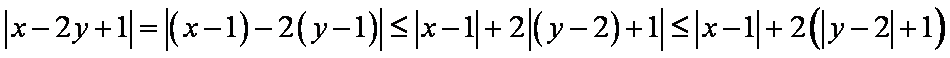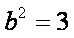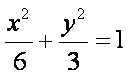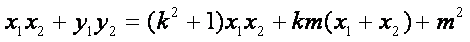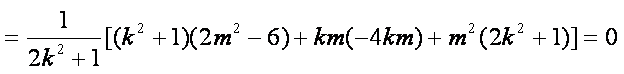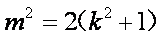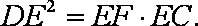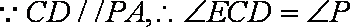- 诱导公式的推导
- 共79题
已知


(1)求
(2)设关于




正确答案
见解析。
解析
(1)由f(x)=

f(x)=(cos








=cosx-sinx=

所以f(x)的最小正周期T=2π.
又由2kπ≤x+


故f(x)的单调递减区间是[-

(2)由f(x)=




又


∴

所以

知识点
已知单位向量



正确答案
答案:1
解析
略
知识点
设函数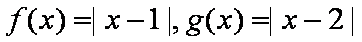
( 1)解不等式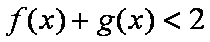
( 2)对于实数
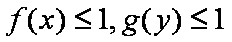
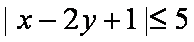
正确答案
见解析
解析
解析:( 1)令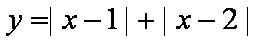
作出函数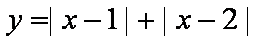
它与直线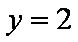
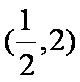
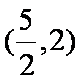
所以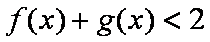

( 2)因为
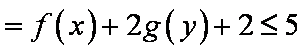
所以 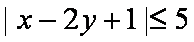
知识点
复数
正确答案
解析
略
知识点
已知椭圆
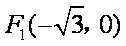
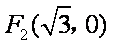
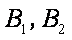
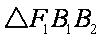
(1) 求椭圆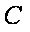
(2) 若直线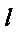
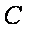
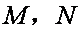
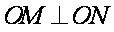
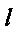
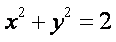
命题意图:本题考查椭圆的方程与性质、直线与二次曲线的位置关系,较难题。
正确答案
见解析。
解析
(1)设椭圆
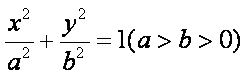
根据题意知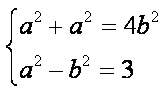
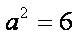
故椭圆
(2)当直线
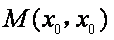
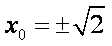
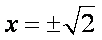
当直线的斜率存在时,设直线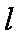
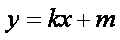
由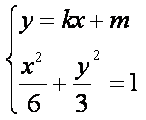
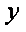
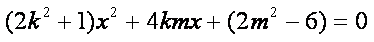
设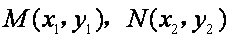
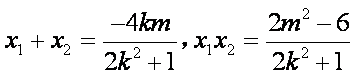
从而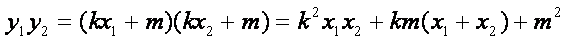
因为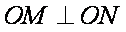
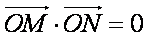
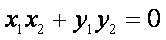
化简得: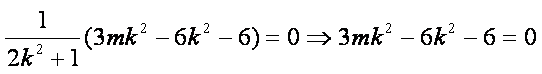
故
另一方面,点
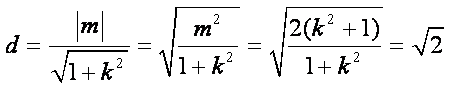
故直线
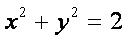
知识点
已知在




(1)求角A、B、C的大小;
(2)设函数

邻两对称轴间的距离。
正确答案
见解析
解析
(1)由题设及正弦定理知:
得
∴



当




当


∴

(2)由(1)及题设知:
当

即

它的相邻两对称轴间的距离为
知识点
当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.某日某省x个监测点数据统计如下:
(1) 根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
(2)若A市共有5个监测点,其中有3个监测点为轻度污染,2个监测点为良.从中任意选取2个监测点,事件A“其 中至少有一个为良”发生的概率是多 少?
正确答案
见解析
解析
解:(1)


(2)设A市空气质量状况属于轻度污染3个监测点为1,2,3,空气质量状况属于良的2个监测点为4,5,从中任取2个的基本事件分别为
(1,2),(1,3),(1,4),(1,5),(2,3),(2,4
其中事件A“其中至少有一个为良”包含的 基本事件为
(1,4),(1,5),(2,4),(2,5),(3,4),(3,5),(4,5)共7种,
所以事件A“其中至少有一个为良”发生的概率是
知识点
设





正确答案
-3
解析
略
知识点
已知复数

正确答案
解析





知识点
如图所示,已知PA是⊙O相切,A为切点,PBC为割线,弦CD//AP,AD、BC相交于E点,F为CE上一点,且
(1)求证:A、P、D、F四点共圆;
(2)若AE·ED=24,DE=
正确答案
见解析
解析
解析:(1)证明: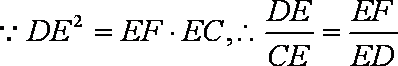
又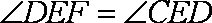
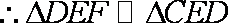
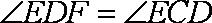
又
故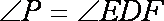
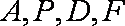
(2)解:由(1)及相交弦定理得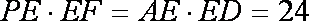
又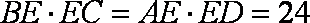

由切割线定理得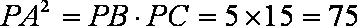
所以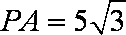
知识点
扫码查看完整答案与解析