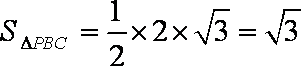诱导公式的推导
共79题

· 诱导公式的推导

诱导公式的推导
共79题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

1.设集合M={x∈R|lgx=0}，N={x∈R|﹣2＜x＜0}，则（　　）

AM⊆N

BM⊇N

CM=N

DM∩N=∅

正确答案

解析

略

知识点

诱导公式的推导

题型：简答题

简答题 · 12 分

对一批共件的某电器进行分类检测，其重量（克）统计如下：

规定重量在克及以下的为“”型，重量在克及以上的为“”型，已知该批电器有“”型件

（1）从该批电器中任选件，求其为“”型的概率；

（2）从重量在的件电器中，任选件，求其中恰有件为“”型的概率

正确答案

见解析

解析

（1）设“从该批电器中任选1件，其为”B”型”为事件， 1分

则 3分

所以从该批电器中任选1件，求其为”B”型的概率为， 4分

（2）设“从重量在[80，85)的5件电器中，任选2件电器，求其中恰有1件为”A”型”为事件，记这5件电器分别为a，b，c，d，e，其中”A”型为a，b，从中任选2件，所有可能的情况为ab，ac，ad，ae，bc，bd，be，cd，ce，de，共10种，

8分

其中恰有1件为”A”型的情况有ac，ad，ae，bc，bd，be，共6种， 10分

所以。

所以从重量在[80，85)的5件电器中，任选2件电器，其中恰有1件为”A”型的概率为， 12分

知识点

诱导公式的推导

题型：简答题

简答题 · 10 分

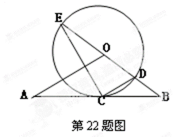
如图，直线AB经过⊙O上的点C，并且OA=OB，CA=CB，⊙O交直线OB于E、D，连结EC、CD.

（1）求证：直线AB是⊙O的切线；

（2）若tan∠CED=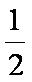,⊙O的半径为3，求OA的长。

正确答案

见解析

解析

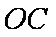
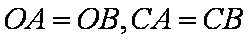
解:（1）连结，因为,则。

所以直线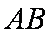是⊙的切线。

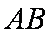
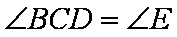
（2）因为是⊙的切线，所以,又,

所以△∽△,所以,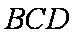

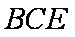
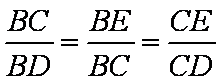
所以,·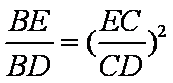

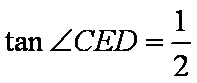
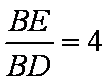
因为,所以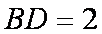,因为⊙的半径为3,

所以,所以

知识点

诱导公式的推导

题型：简答题

简答题 · 10 分

在极坐标系内，已知曲线的方程为，以极点为原点，极轴方向为正半轴方向，利用相同单位长度建立平面直角坐标系，曲线的参数方程为（为参数）。

（1）求曲线的直角坐标方程以及曲线的普通方程；

（2）设点为曲线上的动点，过点作曲线的两条切线，求这两条切线所成角余弦值的取值范围。

正确答案

见解析

解析

（1）对于曲线的方程为，

可化为直角坐标方程，即；

对于曲线的参数方程为（为参数），

可化为普通方程；

（2）过圆心点作直线的垂线，此时两切线成角最大，即余弦值最小，则由点到直线的距离公式可知，

，则，因此，

因此两条切线所成角的余弦值的取值范围是。

知识点

诱导公式的推导

题型：单选题

单选题 · 5 分

若点是圆的弦AB的中点，则直线AB的方程为

正确答案

解析

略

知识点

诱导公式的推导

题型：填空题

填空题 · 4 分

已知数列满足：对任意均有（为常数，且），若，写出一个满足条件的的值为

正确答案

或或

解析

略

知识点

诱导公式的推导

题型：简答题

简答题 · 14 分

如图，设抛物线的焦点为，准线为，过准线上一点且斜率为的直线交抛物线于两点，线段的中点为，直线交抛物线于两点。

（1）求抛物线的方程；

（2）若，试写出关

于的函数解析式，并求实数的取值范围。

正确答案

见解析

解析

（1）抛物线方程为。

（2）设方程为，

由得，

，

代入方程得：

所以，

且直线，

由得，

则得

代入直线方程得

所以，

则，

令，则

而

所以

知识点

诱导公式的推导

题型：简答题

简答题 · 12 分

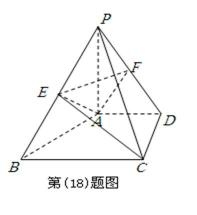
18.已知如图，四边形ABCD是直角梯形，AD//BC，CD⊥AD，PA⊥平面ABCD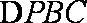，是边长为2的正三角形，BC＝2AD＝2CD，E、F分别是PB、PD的中点.

（Ⅰ）求证:BD//平面AEF；

（Ⅱ）求点A到平面PBC的距离.

正确答案

见解析。

解析

（Ⅰ）证明：连接BD，因为E、F分别是PB、PD的中点.在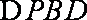中，EF//BD，又因为所以BD//平面AEF。

（Ⅱ）设A到平面PBC的距离为d，因为，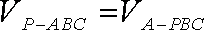

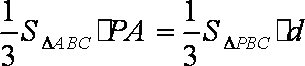
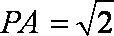
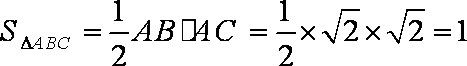
即，又有题意可知，

所以

知识点

诱导公式的推导

题型：单选题

单选题 · 5 分

3．“”是“”的（）

A充分不必要条件

B必要不充分条件

C充要条件

D既不充分也不必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

诱导公式的推导

题型：单选题

单选题 · 5 分

8.已知双曲线的右焦点与抛物线的焦点重合，则该双曲线的一条渐近线方程为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

诱导公式的推导

继续学习学习下一知识点

下一知识点 : 诱导公式的作用

百度题库 > 高考 > 文科数学 > 诱导公式的推导

扫码查看完整答案与解析