解三角形的实际应用
共67题

· 解三角形的实际应用

解三角形的实际应用
共67题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 13 分

17．在ABC中，

（I）求的值：

（II）设AC=，求ABC的面积。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数中的恒等变换应用正弦定理解三角形的实际应用

题型：填空题

填空题 · 5 分

13.在中，两中线与相互垂直，则的最大值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

解三角形的实际应用

题型：填空题

填空题 · 5 分

5．底面边长为2m，高为1m的正三棱锥的全面积为（）m2

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

解三角形的实际应用

题型：单选题

单选题 · 5 分

4.已知f（x）是定义在R上的可导函数,f'（x）为f（x）的导函数,又有两个向量m=（f（x）,-1）,n=（1,f'（x））,且对于x∈R,两向量m,n的夹角范围都是[0,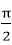）,则（　　）.

Ae2014f（-2014）<f（0）,f（2015）>e2015f（0）

Be2014f（-2014）<f（0）,f（2015）<e2015f（0）

Ce2014f（-2014）>f（0）,f（2015）>e2015f（0）

De2014f（-2014）>f（0）,f（2015）<e2015f（0）

正确答案

解析

因为向量m,n的夹角范围都是[0,),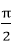

所以m·n=(f(x),-1)·(1,f'(x))=f(x)-f'(x)>0,

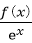
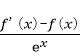
令F(x)=,则F'(x)=<0,

所以F(x)=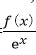为定义在R上的减函数,

所以F(2015)<F(0),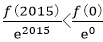,所以f(2015)<e2015f(0).

F(-2014)>F(0),,所以e2014f(-2014)>f(0)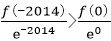

知识点

解三角形的实际应用

题型：简答题

简答题 · 3 分

7．某船在海平面处测得灯塔在北偏东方向，与相距海里.船由向正北方向航行海里达到处，这时灯塔与船相距___________海里（精确到0.1海里）

正确答案

解析

由题可知，AB=6,AC=8.1,A=30o，可求得BC=。

考查方向

本题主要考查了解三角形的实际应用举例。

解题思路

本题考查余弦定理，解题步骤如下：利用余弦定理求解。

易错点

本题要注意余弦定理。

知识点

解三角形的实际应用

继续学习学习下一知识点

下一知识点 : 三角函数的最值

百度题库 > 高考 > 理科数学 > 解三角形的实际应用

扫码查看完整答案与解析