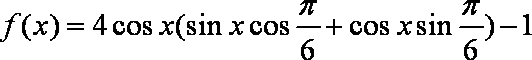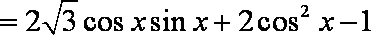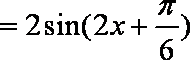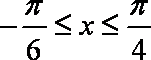两角和与差的正弦函数
共46题

· 两角和与差的正弦函数

两角和与差的正弦函数
共46题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

在锐角△ABC中，已知内角A、B、C所对的边分别为a、b、c，且满足.

(1)求B的大小；

(2)如果b=，求△ABC的面积S△ABC。

正确答案

见解析。

解析

(1)解：

∵0<2B<π，，

(2)由

∵b=，，由余弦定理，得：

解得（舍去负根）

∴ ( 面积单位 )

知识点

两角和与差的正弦函数二倍角的正弦正弦定理

题型：简答题

简答题 · 14 分

已知a，b，c分别是△ABC的三个内角A，B，C的对边，若向量，，且∥。

（1）求角A的大小；

（2）求函数的值域。

正确答案

见解析。

解析

（1）因为向量，，且∥。

所以（2b﹣c）cosA=acosC，由正弦定理得：2sinBcosA=sinCcosA+sinAcosC=sin（A+C）

即2sinBcosA=sinB，所以cosA=，A是三角形的内角，所以A=。

（2）因为函数=sinB+cosB=2sin（B+），

而，所以函数y=2sin（B+）的值域（1，2]。

知识点

两角和与差的正弦函数正弦定理平面向量共线（平行）的坐标表示

题型：简答题

简答题 · 14 分

如图，在直角坐标系xOy中，锐角△ABC内接于圆x2+y2=1.已知BC平行于x轴，AB所在直线方程为y=kx+m（k＞0），记角A，B，C所对的边分别是a，b，c。

（1）若的值；

（2）若的值。

正确答案

见解析。

解析

（1）变式得：，

原式=；

（2）

知识点

三角函数的恒等变换及化简求值两角和与差的正弦函数直线与圆的位置关系

题型：简答题

简答题 · 12 分

已知函数

（1）求函数的定义域和最小正周期；

（2）若求的值。

正确答案

见解析。

解析

（1）由解得，

所以函数的定义域为--

的最小正周期-

（2）解法1：由-

且，-

∴-

【解法2：由得，

代入得，

∴，又，-

∴

知识点

三角函数的周期性及其求法正弦函数的定义域和值域两角和与差的正弦函数二倍角的正弦

题型：简答题

简答题 · 12 分

已知函数, .

（1）求函数的最小正周期；

（2）当时，求函数的值域以及函数的单调区间。

正确答案

（1）（2），

解析

解析：

（2）因为，所以 ,所以

函数的增区间为，减区间为

知识点

三角函数的周期性及其求法正弦函数的定义域和值域正弦函数的单调性三角函数中的恒等变换应用两角和与差的正弦函数

题型：单选题

单选题 · 5 分

的值为

正确答案

解析

原式，故选C。

知识点

诱导公式的作用两角和与差的正弦函数

题型：简答题

简答题 · 12 分

已知函数（为常数）。

（1）求函数的最小正周期和单调增区间；

（2）若函数的图像向左平移个单位后，得到函数的图像关于轴对称，求实数的最小值

正确答案

见解析。

解析

（1）

……3分

的最小正周期为 …………4分

当，即时，

函数单调递增，故所求区间为 …………7分

（2）函数的图像向左平移个单位后得，要使的图像关于轴对称，只需 ………9分

即，所以的最小值为，………………12分

知识点

三角函数的周期性及其求法正弦函数的单调性函数y=Asin（ωx+φ）的图象变换三角函数中的恒等变换应用两角和与差的正弦函数

题型：简答题

简答题 · 14 分

已知，。

（1）求的值；

（2）求的值。

正确答案

见解析。

解析

（1）∵，

∴

；

（2）∵

∴。

知识点

同角三角函数间的基本关系三角函数的化简求值两角和与差的余弦函数两角和与差的正弦函数

题型：填空题

填空题 · 5 分

已知，若，则sin（α﹣β）的值为　　。

正确答案

。

解析

∵α，β∈（，），

∴＜α+＜π，﹣＜β﹣＜0，

又sin（α+）=，cos（β﹣）=，

∴cos（α+）=﹣，sin（β﹣）=﹣。

∴sin（α﹣β）=﹣sin[（α+）﹣（β﹣）]

=﹣[sin（α+）•cos（β﹣）﹣cos（α+）•sin（β﹣）]

=﹣[×﹣（﹣）×（﹣）]

=。

知识点

三角函数的恒等变换及化简求值两角和与差的正弦函数角的变换、收缩变换

题型：简答题

简答题 · 12 分

已知函数，求在区间上的值域。

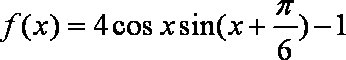
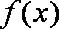
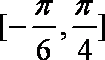
正确答案

见解析。

解析

∵

∴

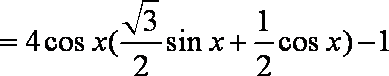
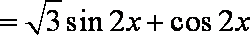
所以，函数在区间的值域是

知识点

正弦函数的定义域和值域三角函数中的恒等变换应用两角和与差的正弦函数

继续学习学习下一知识点

下一知识点 : 两角和与差的正切函数

百度题库 > 高考 > 文科数学 > 两角和与差的正弦函数

扫码查看完整答案与解析