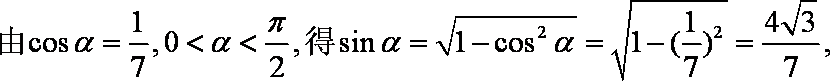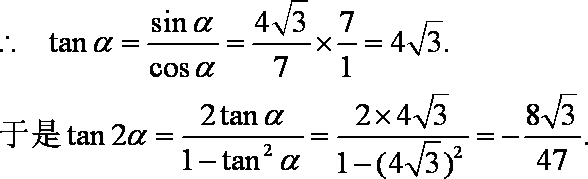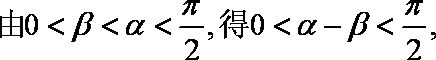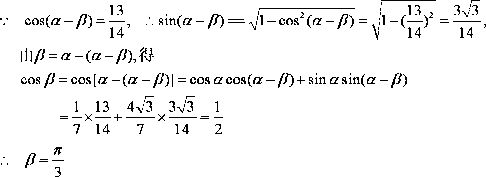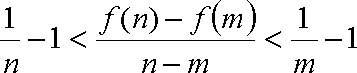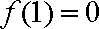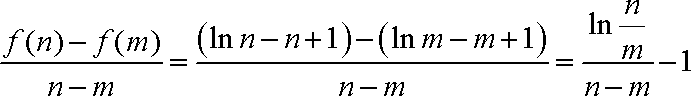- 求函数y=Asin(ωx+φ)的解析式
- 共127题
1
题型:简答题
|
已知



(1)求证:数列

(2)设数列



正确答案
见解析。
解析
(1)

所以




(2) 

对于任意的





知识点
求函数y=Asin(ωx+φ)的解析式
1
题型:简答题
|
已知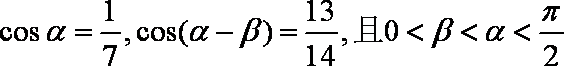
(1)求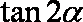
(2)求β。
正确答案
见解析。
解析
(1)
(2)
知识点
求函数y=Asin(ωx+φ)的解析式
1
题型:简答题
|
已知

(1)求角C;
(2)求
正确答案
见解析
解析
(1)
又
(2)
知识点
求函数y=Asin(ωx+φ)的解析式
1
题型:简答题
|
已知数列



(1)若

(2)设




正确答案
见解析。
解析
(1)若




两边取对数,得
化为
因为
所以数列


所以

(2)由

当

①

由已知


因为


所以

因为

所以

知识点
求函数y=Asin(ωx+φ)的解析式
1
题型:简答题
|
已知函数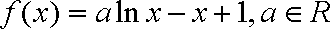
(1)求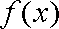
(2)若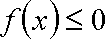
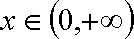
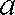
(3)对任意的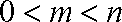
正确答案
见解析
解析
(1)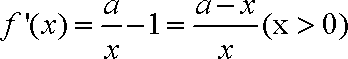
当
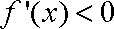
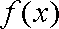
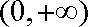
当
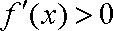
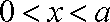
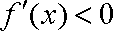

∴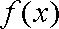
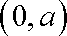
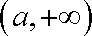
(2)由(1)知:当
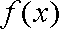
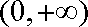
∴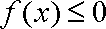
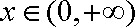
当
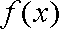
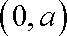
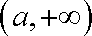
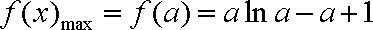
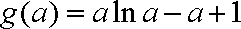
依题意有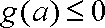
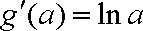
∴
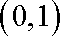
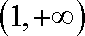
∴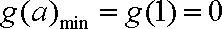
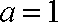
(3)由(2)知: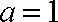
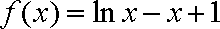
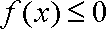
即
则
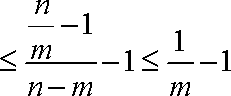
又由
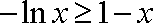
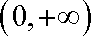
∴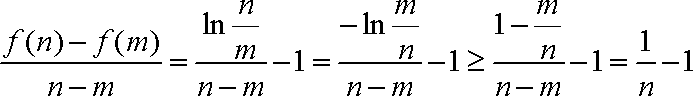
综上所述:对任意的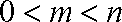
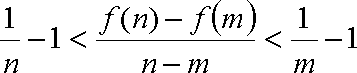
知识点
求函数y=Asin(ωx+φ)的解析式
下一知识点 : 函数y=Asin(ωx+φ)的应用
扫码查看完整答案与解析