- 相关点法求轨迹方程
- 共18题
已知函数

(1)若曲线



(2)当



(3)设


正确答案
见解析。
解析
(1)∵




(2)解法一:令

当




当



对


当





而
综上得对

解法二:由


由于

由图象可知

故当

(3)证法一:由
得

由

又
∴
∵
∵

由①、②、③得
即
【证法二:由
∵
∴
∴
∴

知识点
已知动圆












(1)求曲线
(2)试探究

(3)记


正确答案
见解析。
解析
(1)设圆心

由于动圆


圆






故圆心


(2)设

由


由




(3)





令








知识点
已知双曲线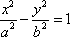
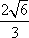
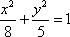
正确答案
解析
略
知识点
平面内与两定点A1(-a,0)、A2(a,0)(a>0)连线的斜率之积等于非零常数m的点的轨迹,加上A1、A2两点所成的曲线C可以是圆、椭圆或双曲线。
(1)求曲线C的方程,并讨论C的形状与m值的关系;
(2)当m=-1时,对应的曲线为C1;对给定的m∈(-1,0)∪(0,+∞),对应的曲线为C2,设F1、F2是C2的两个焦点,试问:在C1上,是否存在点N,使得△F1NF2的面积S=|m|a2,若存在,求tan∠F1NF2的值;若不存在,请说明理由。
正确答案
见解析。
解析
知识点
19,已知曲线C的方程为:
(1)判断曲线C的形状;
(2)设曲线C分别与x轴、y轴交于点A、B(A、B不同于原点O),试判断△AOB的面积S是否为定值?并证明你的判断;
(3)设直线

正确答案
见解析。
解析
(1) 将曲线C的方程化为
可知曲线C是以点

(2)△AOB的面积S为定值,
证明如下:
在曲线C的方程中令y=0得
在曲线C的方程中令x=0得

∴
(3)∵圆C过坐标原点,且
∴圆心


当


圆心到直线

直线
∴

知识点
扫码查看完整答案与解析