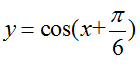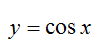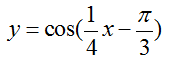- 弧度制的应用
- 共31题
1
题型:
单选题
|
将函数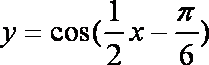
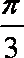
正确答案
C
解析
略
知识点
弧度制的应用
1
题型:
单选题
|
10.对定义在


(i) 对任意的

(ii) 当

则下列四个函数中不是
① 
②
③ 
④
正确答案
A
解析
(i)在

对于①,
对于②,

对于③,




∴

对于④,

故选A.
知识点
弧度制的应用
1
题型:
单选题
|
5. 已知函数

正确答案
B
解析
解析已在路上飞奔,马上就到!
知识点
弧度制的应用
1
题型:
单选题
|
3.已知直线


正确答案
C
解析
解析已在路上飞奔,马上就到!
知识点
弧度制的应用
1
题型:简答题
|
16.甲和乙参加智力答题活动,活动规则:
①答题过程中,若答对则继续答题;若答错则停止答题;
②每人最多答3个题;
③答对第一题得10分,第二题得20分,第三题得30分,答错得0分.
已知甲答对每个题的概率为

(1)求甲恰好得30分的概率;
(2)设乙的得分为

(3)求甲恰好比乙多30分的概率.
正确答案
(1)甲恰好得30分,说明甲前两题都答对,而第三题答错,其概率为
(2)



(3)设甲恰好比乙多30分为事件

甲恰好得60分且乙恰好得30分为事件




所以,甲恰好比乙多30分的概率为
解析
解析已在路上飞奔,马上就到!
知识点
弧度制的应用
下一知识点 : 弧长公式
扫码查看完整答案与解析