- 频率分布表
- 共23题
3.某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是

正确答案
知识点
某险种的基本保费为
设该险种一续保人一年内出险次数与相应概率如下:
19.求一续保人本年度的保费高于基本保费的概率;
20.若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
21.求续保人本年度的平均保费与基本保费的比值.
正确答案
(Ⅰ)0.55;
解析
试题分析:本题属于概率与统计综合应用问题,属于简单题,只要掌握相关概率与统计的知识,即可解决本题,解析如下:
试题解析:(Ⅰ)设

考查方向
解题思路
(Ⅰ)根据互斥事件的概率公式求一续保人本年度的保费高于基本保费的概率;
易错点
相关知识点不熟容易出错。
正确答案
(Ⅱ)
解析
试题分析:本题属于概率与统计综合应用问题,属于简单题,只要掌握相关概率与统计的知识,即可解决本题,解析如下:
(Ⅱ)设


又
因此所求概率为
考查方向
解题思路
(Ⅱ)一续保人本年度的保费高于基本保费,当且仅当一年内出险次数大于3,由条件概率公式求解;
易错点
相关知识点不熟容易出错。
正确答案
(Ⅲ)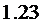
解析
试题分析:本题属于概率与统计综合应用问题,属于简单题,只要掌握相关概率与统计的知识,即可解决本题,解析如下:
⑶解:设本年度所交保费为随机变量
平均保费

∴平均保费与基本保费比值为
考查方向
解题思路
(Ⅲ)记续保人本年度的保费为

易错点
相关知识点不熟容易出错。
2015年8月12日天津发生危化品重大爆炸事故,造成重大人员和经济损失.某港口组织消防人员对该港口的公司的集装箱进行安全抽检,已知消防安全等级共分为四个等级(一级为优,二级为良,三级为中等,四级为差),该港口消防安全等级的统计结果如下表所示:


19.求
20.按消防安全等级利用分层抽样的方法从这
正确答案
详见解析
解析
(Ⅰ)由已知可得;0.30+2m+m+0.10=1,解得:m=0.20. ……………………2分
所以
考查方向
概率和统计的计算
解题思路
按照统计的相关数据计算
易错点
数据不敏感,计算错误
正确答案
详见解析
解析
(Ⅱ)由(Ⅰ)知,利用分层抽样的方法从中抽取10家公司,则消防安全等级为一级的有3家,二级的有4家,三级的有2家,四级的有1家. ……………………6分
记消防安全等级为二级的4家公司分别为A,B,C,D,三级的2家公司分别记为











记“抽取的2家公司的消防安全等级都是二级”为事件M,则事件M包含的结果有:(A,B)(A,C)(A,D)(B,C)(B,D)(C,D)…共6种,……………………10分
所以
考查方向
分层抽样,随机事件发生的概率
解题思路
分情况讨论所可能发生的情况,然后计算概率
易错点
先求出所有出现的可能,然后算题目要求的可能,求二者的比例
扫码查看完整答案与解析





















