三角函数中的恒等变换应用
共286题

· 三角函数中的恒等变换应用

三角函数中的恒等变换应用
共286题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

16.已知函数（）.

（1）求函数的最大值，并指出取得最大值时相应的的值；

（2）设，若是偶函数,求的值.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的奇偶性三角函数中的恒等变换应用诱导公式的作用三角函数的最值

题型：填空题

填空题 · 5 分

14.若函数的图象在处的切线方程是，则（）.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数中的恒等变换应用

题型：简答题

简答题 · 10 分

17. 已知函数f(x)＝2sinxcos(x＋)－cos2x＋m.

（1）求函数f(x)的最小正周期；

（2）当时，函数f(x)的最小值为－3，求实数m的值

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法三角函数中的恒等变换应用三角函数的最值

题型：简答题

简答题 · 13 分

15．已知函数,.

（1）求函数的最小正周期与单调增区间；

（2）求函数在上的最大值与最小值.

正确答案

解： .

（1）的最小正周期为

令，解得，

所以函数的单调增区间为.

（2）因为，所以，所以，

于是，所以.

当且仅当时取最小值

当且仅当，即时最大值.

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法正弦函数的定义域和值域正弦函数的单调性三角函数中的恒等变换应用

题型：填空题

填空题 · 4 分

5．函数的图象上相邻二条对称轴之间的距离是（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的对称性三角函数中的恒等变换应用

题型：单选题

单选题 · 5 分

8．设，其中，若对一切恒成立，则下列结论正确的是（）

① ；

② 既不是奇函数也不是偶函数；

③ 的单调递增区间是；

④ 存在经过点的直线与函数的图象不相交.

A①②

B①③

C②③

D②④

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用正弦函数的奇偶性正弦函数的单调性三角函数中的恒等变换应用不等式恒成立问题

题型：简答题

简答题 · 13 分

18．

已知向量，，定义函数f（x）=。

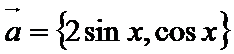
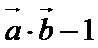
（1）求函数f（x）的最小正周期。

（2）x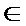R时求函数f（x）的最大值及此时的x值。

正确答案

f（x）=-1=2sinx×cosx+2cosx-1=sin2x+cos2x=2sin（2x+），

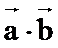
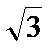
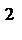
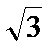
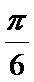
（1）T== ，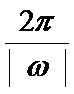

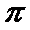
（2）f（x）=2sin（2x+），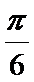

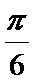
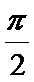
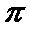
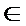
∴当2x+=+2k （kZ），

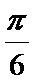
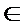
即x=+k （kZ）时，f（x）取最大值为2，

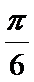
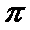
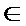
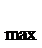
∴当x=+k （kZ）时f（x）=2 。

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法三角函数中的恒等变换应用三角函数的最值平面向量数量积的运算

题型：单选题

单选题 · 5 分

2．设则的大小关系是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的单调性三角函数中的恒等变换应用

题型：简答题

简答题 · 12 分

20．如图，四棱锥中，底面是矩形，底面，，，点是的中点，点在边上移动．

（1）点为的中点时，试判断与平面的位置关系，并说明理由；

（2）求证：无论点在边的何处，都有；

（3）当为何值时,与平面所成角的大小为45°.

正确答案

.解：（1）当点E为BC的中点时，EF与平面PAC平行．

∵在△PBC中，E、F分别为BC、PB的中点，

∴EF∥PC.

又EF⊄平面PAC，而PC⊂平面PAC，

∴EF∥平面PAC.

（2）

证明：建立如图所示空间直角坐标系，则

(3)设平面PDE的法向量为

解析

解析已在路上飞奔，马上就到！

知识点

三角函数中的恒等变换应用

题型：简答题

简答题 · 12 分

18.已知函数

（1）求的最小正周期和单调区间；

（2）若求的取值范围；

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法正弦函数的定义域和值域正弦函数的单调性三角函数中的恒等变换应用

继续学习学习下一知识点

下一知识点 : 诱导公式的推导

百度题库 > 高考 > 理科数学 > 三角函数中的恒等变换应用

扫码查看完整答案与解析