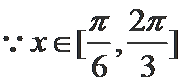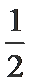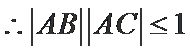- 三角函数中的恒等变换应用
- 共286题
已知函数


15.求
16.求


正确答案
1;
解析
试题分析:本题属于三角公式与三角函数综合应用问题,题目的难度适中。(1)化简时一定要结合半倍角公式及辅助角公式灵活应用;(2)第二问属于给定区间求三角函数最值问题,只要注意此种问题的方法即可。
(Ⅰ)

因为


考查方向
解题思路
由已知利用半角公式与辅助角公式对
第二问按照“给定区间”求函数最值的方法结合正弦函数的性质得出f(x)的最值。
易错点
本题在第一问对


正确答案
(2)最大值为

解析
试题分析:本题属于三角公式与三角函数综合应用问题,题目的难度适中。(1)化简时一定要结合半倍角公式及辅助角公式灵活应用;(2)第二问属于给定区间求三角函数最值问题,只要注意此种问题的方法即可。
(Ⅱ)由(Ⅰ)可知
因为

则
当



当







考查方向
解题思路
由已知利用半角公式与辅助角公式对
第二问按照“给定区间”求函数最值的方法结合正弦函数的性质得出f(x)的最值。
易错点
本题在第一问对


已知
17.若







正确答案
解析
(Ⅰ)



考查方向
解题思路
化简


易错点
通过降幂公式、辅助角公式化简

正确答案

解析









考查方向
解题思路
化简


易错点
通过降幂公式、辅助角公式化简

已知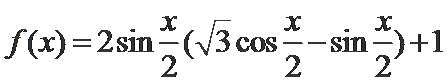
17.若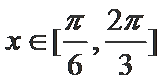
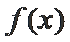

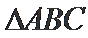
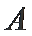
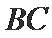
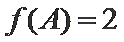
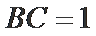
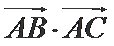
正确答案
(1)值域为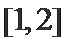
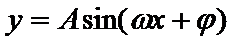
解析
(Ⅰ)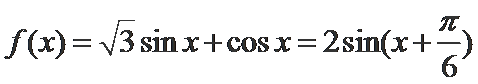

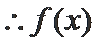
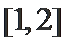
解题思路
利用降幂公式、辅助角公式把函数化成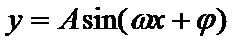
利用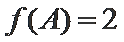
易错点
求值域时,直接带定义域的端点求最值
第2问没能联想到基本不等式求最值。
正确答案
最大值为
解析
(Ⅱ)
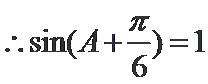
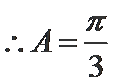
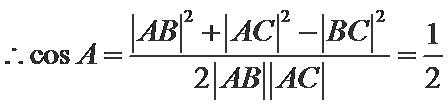
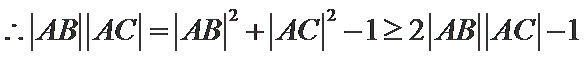
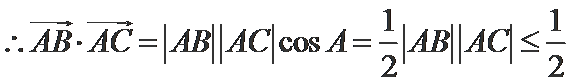
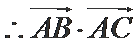
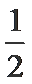
考查方向
解题思路
利用降幂公式、辅助角公式把函数化成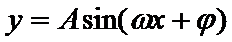
利用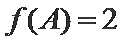
易错点
求值域时,直接带定义域的端点求最值
第2问没能联想到基本不等式求最值。
8.已知tanα=﹣2,tan(α+β)=
正确答案
3
解析
:tanα=﹣2,tan(α+β)=


即

故答案为:3.
考查方向
解题思路
直接利用两角和的正切函数,求解即可.
易错点
本题考查两角和的正切函数,用公式计算时易错.
知识点
3.若

正确答案
解析
因为
所以
考查方向
三角函数的化简求值
解题思路
利用正弦与余弦关系化简
易错点
对相关等式化简掌握不牢固
知识点
9.若将函数


正确答案
解析
由

又所得图象关于y轴对称,则
∴当k=-1时,

故选C.
考查方向
解题思路
把函数式



易错点
三角函数图象的平移应遵循“左加右减”的原则.
知识点
7.若


正确答案
解析

联立可得
考查方向
三角函数
解题思路
三角恒等变换得到
由a所在象限再进行计算。
易错点
不注意角的象限
教师点评
本题难度中等,要求学生能够熟练应用三角函数化简与恒等变换和计算。
知识点
扫码查看完整答案与解析