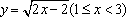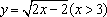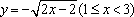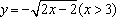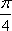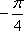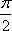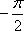函数概念与表示
共2805题

函数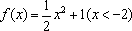概念与表示
共2805题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 4 分

函数的反函数是　　　（　）

正确答案

解析

略

知识点

函数的概念及其构成要素

题型：单选题

单选题 · 5 分

设函数与函数的对称轴完全相同，则的值为

正确答案

解析

略

知识点

函数的概念及其构成要素

题型：填空题

填空题 · 5 分

已知函数，且函数有且仅有两个零点，则实数的取值范围是。

正确答案

解析

略

知识点

函数的概念及其构成要素

题型：单选题

单选题 · 5 分

已知函数，则函数（）的零点个数不可能为

正确答案

解析

略

知识点

函数的概念及其构成要素

题型：填空题

填空题 · 5 分

已知函数若，使得成立，则实数的取值范围是。

正确答案

解析

略

知识点

函数的概念及其构成要素

题型：单选题

单选题 · 5 分

已知，，规定：当时, ；当时, ，则

A有最小值-1,最大值1

B有最大值1,无最小值

C有最小值,无最大值

D有最大值-1,无最小值

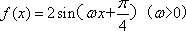
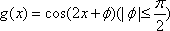
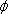
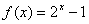
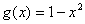
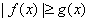
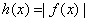
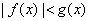
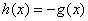
正确答案

解析

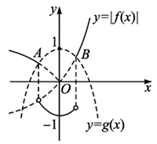
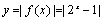
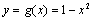
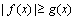
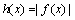
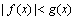
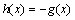
画出与的图象,它们交于A、B两点.由“规定”，在A、B两侧, 故；在A、B之间, ,故.

综上可知, 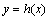的图象是图中的实线部分,因此有最小值-1,无最大值.

知识点

函数的概念及其构成要素

题型：填空题

填空题 · 5 分

如图3，AB的延长线上任取一点C，过C作圆的切线CD，切点为D，的平分线交AD于E,则 ____ .

正确答案

45°

解析

连接，与相交于点，设，

,，，

，，而，45°。

知识点

函数的概念及其构成要素

题型：填空题

填空题 · 5 分

设a为常数，函数，若在上是增函数，则的取值范围是　。

正确答案

解析

略

知识点

函数的概念及其构成要素

题型：简答题

简答题 · 14 分

已知函数

（1）求此函数的单调区间及最值；

（2）求证：对于任意正整数n，均有（为自然对数的底数）；

（3）当a＝1时，是否存在过点（1，－1）的直线与函数的图象相切？若存在，有多少条？若不存在，说明理由。

正确答案

见解析。

解析

（1）解：由题意， ………………1分

当时，函数的定义域为，

此时函数在上是减函数，在上是增函数，

，无最大值，………………3分

当时，函数的定义域为，

此时函数在上是减函数，在上是增函数，

，无最大值，………………5分

（2）取，由⑴知，

故，

取，则，………………9分

（3）假设存在这样的切线，设其中一个切点，

∴切线方程：，将点坐标代入得：

，即， ①

设，则，………………12分

，

在区间，上是增函数，在区间上是减函数，

故。

又，

注意到在其定义域上的单调性，知仅在内有且仅有一根

方程①有且仅有一解，故符合条件的切线有且仅有一条，…………14分

知识点

函数的概念及其构成要素

题型：单选题

单选题 · 5 分

若对于定义在上的函数，其函数图象是连续的，且存在常数（），使得对任意的实数x成立，则称是“同伴函数”，下列关于“同伴函数”的叙述中正确的是

A“同伴函数”至少有一个零点

B是一个“同伴函数”

C是一个“同伴函数”

D是唯一一个常值“同伴函数”

正确答案

解析

A正确，令，得，所以，若，显然有实数根；若，，又因为的函数图象是连续不断，所以在上必有实数根，因此任意的“同伴函数”必有根，即任意“同伴函数”至少有一个零点。

B错误，用反证法，假设是一个“同伴函数”，则，即对任意实数x成立，所以，而此式无解，所以不是一个“同伴函数”。

C错误.因为的定义域不是R.

D错误，设是一个“同伴函数”，则，当时，可以取遍实数集，因此不是唯一一个常值“同伴函数”。

知识点

函数的概念及其构成要素

继续学习学习下一知识点

下一知识点 : 函数的基本性质

百度题库 > 高考 > 理科数学 > 函数概念与表示

扫码查看完整答案与解析