统计与统计案例_章节学习

1

题型：填空题

|

填空题 · 12 分

（本小题满分12分）

我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准（吨）、一位居民的月用水量不超过的部分按平价收费，超出的部分按议价收费.为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0,0.5)，[0.5,1)，…，[4,4.5)分成9组，制成了如图所示的频率分布直方图.

（I）求直方图中a的值；

（II）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；

（III）若该市政府希望使85%的居民每月的用水量不超过标准（吨），估计的值，并说明理由.

正确答案

（Ⅰ）由频率分布直方图知，月均用水量在[0,0.5)中的频率为0.08×0.5=0.04，

同理，在[0.5,1)，[1.5,2)，[2,2.5)，[3,3.5)，[3.5,4)，[4,4.5)中的频率分别为0.08，0.20，0.26，0.06，0.04，0.02．

由0.04+0.08+0.5×a+0.20+0.26+0.5×a+0.06+0.04+0.02=1，

解得a=0.30．

（Ⅱ）由（Ⅰ），100位居民每人月均用水量不低于3吨的频率为0.06+0.04+0.02=0.12．

由以上样本的频率分布，可以估计全市30万居民中月均用水量不低于3吨的人数为

300 000×0.12=36 000．

（Ⅲ）因为前6组的频率之和为0.04+0.08+0.15+0.20+0.26+0.15=0.88>0.85，

而前5组的频率之和为0.04+0.08+0.15+0.20+0.26=0.73<0.85，

所以2.5≤x<3．

由0.3×(x–2.5)=0.85–0.73，

解得x=2.9．

所以，估计月用水量标准为2.9吨时，85%的居民每月的用水量不超过标准．

知识点

频率分布直方图用样本的频率分布估计总体分布随机抽样和样本估计总体的实际应用

1

题型：简答题

|

简答题 · 12 分

我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准（吨）、一位居民的月用水量不超过的部分按平价收费，超出的部分按议价收费.为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0,0.5)，[0.5,1)，…，[4,4.5)分成9组，制成了如图所示的频率分布直方图.

16.求直方图中a的值；

17.设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；

18.若该市政府希望使85%的居民每月的用水量不超过标准（吨），估计的值，并说明理由.

第(1)小题正确答案及相关解析

正确答案

（Ⅰ）；

解析

（I）由概率统计相关知识，各组频率之和的值为1

∵频率=(频率/组距)*组距

∴

得

考查方向

本题主要考查频率分布直方图、频率、频数的计算公式等基础知识，考查学生的分析问题解决问题的能力.

解题思路

本题主要考查频率分布直方图、频率、频数的计算公式等基础知识，考查学生的分析问题解决问题的能力.在频率分布直方图中，第个小矩形面积就是相应的频率或概率，所有小矩形面积之和为1，这是解题的关键，也是识图的基础．

易错点

本题主要在计算中易错

第(2)小题正确答案及相关解析

正确答案

（Ⅱ）36000；

解析

（II）由图，不低于3吨人数所占百分比为

∴全市月均用水量不低于3吨的人数为：(万)

考查方向

本题主要考查频率分布直方图、频率、频数的计算公式等基础知识，考查学生的分析问题解决问题的能力.

解题思路

本题主要考查频率分布直方图、频率、频数的计算公式等基础知识，考查学生的分析问题解决问题的能力.在频率分布直方图中，第个小矩形面积就是相应的频率或概率，所有小矩形面积之和为1，这是解题的关键，也是识图的基础．

易错点

本题主要在计算中易错

第(3)小题正确答案及相关解析

正确答案

（Ⅲ）2.9

解析

（Ⅲ）因为前6组的频率之和为0.04+0.08+0.15+0.20+0.26+0.15=0.88>0.85，

而前5组的频率之和为0.04+0.08+0.15+0.20+0.26=0.73<0.85，

所以2.5≤x<3．

由0.3×(x–2.5)=0.85–0.73，

解得x=2.9．

所以，估计月用水量标准为2.9吨时，85%的居民每月的用水量不超过标准．

考查方向

本题主要考查频率分布直方图、频率、频数的计算公式等基础知识，考查学生的分析问题解决问题的能力.

解题思路

本题主要考查频率分布直方图、频率、频数的计算公式等基础知识，考查学生的分析问题解决问题的能力.在频率分布直方图中，第个小矩形面积就是相应的频率或概率，所有小矩形面积之和为1，这是解题的关键，也是识图的基础．

易错点

本题主要在计算中易错

1

题型：填空题

|

填空题 · 5 分

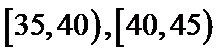
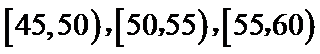
11.某高校为了了解教科研工作开展状况与教师年龄之间的关系，将该校不小于35岁的80名教师按年龄分组，分组区间为，，由此得到频率分布直方图如图，则这80名教师中年龄小于45岁的教师有________人.

正确答案

48

解析

这80名教师中年龄小于45岁的教师频率为：（0.04+0.08）×5=0.6

这80名教师中年龄小于45岁的教师人数为：0.6×80=48．

考查方向

本题主要考查了频率分布直方图

解题思路

根据直方图中的各个矩形的面积代表了频率，先求出年龄小于45的教师的频率，再根据频率与频数的关系进行求解．

易错点

本题必须注意直方图中的各个矩形的面积代表了频率，频数=频率×样本容量．

知识点

频率分布直方图

1

题型：单选题

|

单选题 · 5 分

3.根据下面给出的2004年至2013年我国二氧化硫排放量（单位：万吨）柱形图。以下结论不正确的是（　　　）

A逐年比较，2008年减少二氧化硫排放量的效果最显著

B2007年我国治理二氧化硫排放显现

C2006年以来我国二氧化硫年排放量呈减少趋势

D2006年以来我国二氧化硫年排放量与年份正相关

正确答案

D

知识点

频率分布直方图

1

题型：简答题

|

简答题 · 12 分

某市规定，高中学生三年在校期间参加不少于小时的社区服务才合格．教育部门在全市随机抽取200位学生参加社区服务的数据，按时间段，，，，（单位：小时）进行统计，其频率分布直方图如图所示．

19.求抽取的200位学生中，参加社区服务时间不少于90小时的学生人数，并估计从全市高中学生中任意选取一人，其参加社区服务时间不少于90小时的概率；

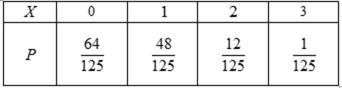
20.从全市高中学生（人数很多）中任意选取3位学生，记为3位学生中参加社区服务时间不少于90小时的人数．试求随机变量的分布列和数学期望和方差．

第(1)小题正确答案及相关解析

正确答案

见解析

解析

根据题意，参加社区服务时间在时间段小时的学生人数为（人），参加社区服务时间在时间段小时的学生人数为（人）．所以抽取的200位学生中，参加社区服务时间不少于90小时的学生人数为人．所以从全市高中学生中任意选取一人，其参加社区服务时间不少于90小时的概率估计为

考查方向

频率分布直方图；随机变量分布列

解题思路

第1问根据样本数据估计总体数据，第2问先把所有可能的情况列出来，然后用频率求概率

易错点

数据收集整理出错

第(2)小题正确答案及相关解析

正确答案

见解析

解析

由19题可知，从全市高中生中任意选取1人，其参加社区服务时间不少于90小

时的概率为由已知得，随机变量的可能取值为．

所以；；

；．

随机变量的分布列为

因为～，所以

考查方向

频率分布直方图；随机变量分布列

解题思路

第1问根据样本数据估计总体数据，第2问先把所有可能的情况列出来，然后用频率求概率

易错点

数据收集整理出错

1

题型：简答题

|

简答题 · 12 分

某学校研究性学习小组对该校高三学生视力情况进行调查，在高三的全体1000名学生中随机抽取了100名学生的体检表，并得到如图的频率分布直方图.

19.若直方图中后四组的频数成等差数列，试估计全年级视力在5.0以下的人数；

20.学习小组成员发现，学习成绩突出的学生，近视的比较多，为了研究学生的视力与学习成绩是否有关系，对年级名次在1～50名和951～1000名的学生进行了调查，得到右表中数据，根据表中的数据，能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?

21.在20题中调查的100名学生中，按照分层抽样在不近视的学生中抽取了9人，进一步调查他们良好的护眼习惯，并且在这9人中任取3人，记名次在1～50的学生人数为，求的分布列和数学期望.

附：

第(1)小题正确答案及相关解析

正确答案

见解析

解析

设各组的频率为，由图可知，第一组有3人，第二组7人，第三组27人，因为后四组的频数成等差数列，所以后四组频数依次为所以视力在5.0以下的频率为3+7+27+24+21=82人，故全年级视力在5.0以下的人数约为

考查方向

分层抽样；随机事件的概率；分布列与期望

解题思路

图和表相互结合求得，先列出可取的所有情况，然后再求期望

易错点

计算错误；读取数据时有遗漏

第(2)小题正确答案及相关解析

正确答案

见解析

解析

，因此在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系

考查方向

分层抽样；随机事件的概率；分布列与期望

解题思路

图和表相互结合求得，先列出可取的所有情况，然后再求期望

易错点

计算错误；读取数据时有遗漏

第(3)小题正确答案及相关解析

正确答案

见解析

解析

依题意9人中年级名次在1～50名和951～1000名分别有3人和6人，

可取0、1、2、3 ，，

，

的分布列为

的数学期望

考查方向

分层抽样；随机事件的概率；分布列与期望

解题思路

图和表相互结合求得，先列出可取的所有情况，然后再求期望

易错点

计算错误；读取数据时有遗漏

1

题型：简答题

|

简答题 · 12 分

某校高二年级共有学生1000名，其中走读生750名，住宿生250名，现采用分层抽样的方法从该年级抽取100名学生进行问卷调查．根据问卷取得了这100名学生每天晚上有效学习时间（单位：分钟）的数据，按照以下区间分为八组：①[0，30），② [30，60），③[60，90），④[90， 120），……得到频率分布直方图（部分）如图（4）．

19.如果把“学生晚上有效时间达到两小时”作为是否充分利用时间的标准，对抽取的100名学生，完成下列2×2列联表；并判断是否有95％的把握认为学生利用时间是否充分与走读、住宿有关?

20.若在第①组、第②组、第③组中共抽出3人调查影响有效利用时间的原因，记抽到“有效学习时间少于60分钟”的学生人数为X，求X的分布列和数学期望．

第(1)小题正确答案及相关解析

正确答案

（1）

由于K2>3.841，所以有95%的把握认为学生利用时间是否充分与走读、住宿有关

解析

解：（1）

K2=≈5.556

由于K2>3.841，所以有95%的把握认为学生利用时间是否充分与走读、住宿有关

考查方向

本题主要考查了独立性检验和分布列，考查考生的运算能力

解题思路

（1）根据走读生和住宿生的样本数完成表格，并由表格计算K2确定相关程度

（2）首先计算出第①组、第②组、第③组各抽取的人数，再确定随机变量X的所有可能取值并计算其概率完成分布列，最后计算数学期望。

易错点

各组人数的确定和离散型随机变量的概率的计算

第(2)小题正确答案及相关解析

正确答案

（2）

解析

（2）设第i组的频率为Pi（i=1,2,…,8),则由图可知：P1=×30=，P2=×30= ，P3=×30=，可得：第①组1人，第②组4人，第③组10人。

则X的所有可能取值为0,1,2,3，

的分布列为：

(或由X服从超几何分布，

考查方向

本题主要考查了独立性检验和分布列，考查考生的运算能力

解题思路

（1）根据走读生和住宿生的样本数完成表格，并由表格计算K2确定相关程度

（2）首先计算出第①组、第②组、第③组各抽取的人数，再确定随机变量X的所有可能取值并计算其概率完成分布列，最后计算数学期望。

易错点

各组人数的确定和离散型随机变量的概率的计算

1

题型：简答题

|

简答题 · 12 分

某企业为了解下属某部门对本企业职工的服务情况，随机访问50名职工，根据这50名职工对该部门的评分，绘制频率分布直方图（如图所示），其中样本数据分组区间为．

19.求频率分布图中的值；

20.估计该企业的职工对该部门评分不低于80的概率；

21.从评分在的受访职工中，随机抽取2人，求此2人评分都在的概率．

第(1)小题正确答案及相关解析

正确答案

，

解析

试题分析：本题属于统计与概率的常见题型，题目的难度是比较稳定，属于中档偏易题，由频率之和为1求解出的值； ∵，∴．

考查方向

本题主要考查了统计、古典概型，常见的还有几何概型。

解题思路

本题主要考查了统计、古典概型，解题步骤如下：由频率之和为1求解出的值。

易错点

审题不清和考虑不全面导致出错。

第(2)小题正确答案及相关解析

正确答案

，

解析

试题分析：本题属于统计与概率的常见题型，题目的难度是比较稳定，属于中档偏易题，由频率估计出相应概率；

由所给频率分布直方图知，50名受访职工评分不低于80的频率为．

∴该企业职工对该部门评分不低于80的概率估计值为

考查方向

本题主要考查了统计、古典概型，常见的还有几何概型。

解题思路

本题主要考查了统计、古典概型，解题步骤如下：由频率估计出相应概率。

易错点

审题不清和考虑不全面导致出错。

第(3)小题正确答案及相关解析

正确答案

；

解析

试题分析：本题属于统计与概率的常见题型，题目的难度是比较稳定，属于中档偏易题，用列举法求出所有基本事件数和符合所求事件数，再算出对应概率。

受访职工评分在的有：（人），记为．

受访职工评分在的有：（人），记为．从这5名受访职工中随机抽取2人，所有可能的结果共有10种，分别是：

．又∵所抽取2人的评分都在的结果有1种，即，故所求的概率为．

考查方向

本题主要考查了统计、古典概型，常见的还有几何概型。

解题思路

本题主要考查了统计、古典概型，解题步骤如下：用列举法求出所有基本事件数和符合所求事件数，再算出对应概率。

易错点

审题不清和考虑不全面导致出错。

1

题型：填空题

|

填空题 · 5 分

4．如图所示，一家面包销售店根据以往某种面包的销售记录，绘制了日销售量的频率分布直方图．若一个月以30天计算，估计这家面包店一个月内日销售量不少于150个的天数为．

正确答案

9

解析

日销售量不少于150的频率：,其对应的天数为

考查方向

本题主要考查了频率分布直方图求概率

解题思路

先计算出日销售量不少于150的频率，然后求出其对应的天数

易错点

本题易对频率分布直方图理解不透，其每个矩形面积就是频率

知识点

频率分布直方图

1

题型：简答题

|

简答题 · 12 分

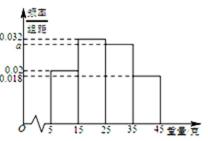
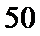
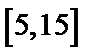
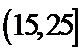
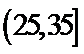
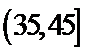
一个盒子中装有大量形状大小一样但重量不尽相同的小球，从中随机抽取个作为样本，称出它们的重量（单位：克），重量分组区间为，，，，由此得到样本的重量频率分布直方图（如图），

19.求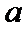的值，并根据样本数据，试估计盒子中小球重量的众数与平均值；

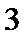
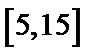
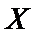
20.从盒子中随机抽取个小球，其中重量在内的小球个数为，求的分布列和数学期望. (以直方图中的频率作为概率).

第(1)小题正确答案及相关解析

正确答案

估计盒子中小球重量的平均值约为克;

解析

（Ⅰ）由题意，得，解得；

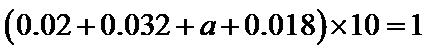
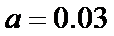
又由最高矩形中点的的横坐标为20，可估计盒子中小球重量的众数约为20（克），

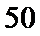
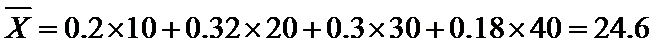
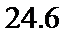
而个样本小球重量的平均值为：（克）故由样本估计总体，可估计盒子中小球重量的平均值约为克；

考查方向

本题主要考查频率分布直方图的知识和二项分布的知识，意在考查考生的处理数据的能力和理解问题、解决问题的能力。

解题思路

根据频率分布直方图求出a的值，然后根据直方图估计盒子中小球重量的众数与平均值；

易错点

不会根据频率分布直方图估计平均数；

第(2)小题正确答案及相关解析

正确答案

（2）的分布列为：

.

（或者）

解析

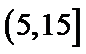
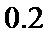
（Ⅱ）利用样本估计总体，该盒子中小球重量在内的概率为，

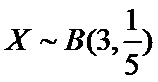
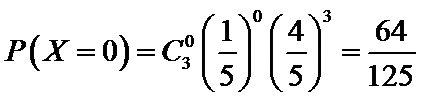
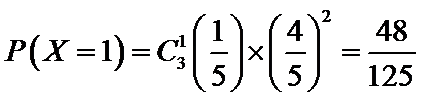
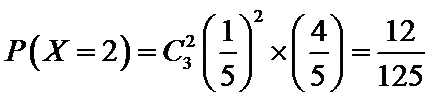
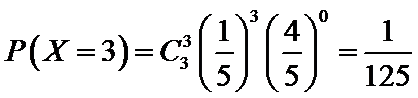
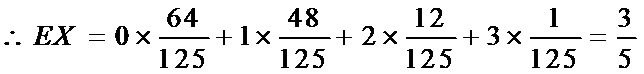
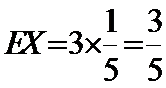
则.的可能取值为、、、，

，，

，.

的分布列为：

.（或者）

考查方向

本题主要考查频率分布直方图的知识和二项分布的知识，意在考查考生的处理数据的能力和理解问题、解决问题的能力。

解题思路

根据题意判断出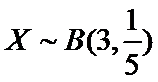，后利用二项分布的知识求出其分布列和期望即可。

易错点

看不出二项分布导致运算很麻烦。

热门试卷

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路