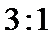- 统计与统计案例
- 共483题
6．某工厂一年中各月份的收入、支出情况的统计如图所示,下列说法中错误的是
A收入最高值与收入最低值的比是
B结余最高的月份是7月
C1至2月份的收入的变化率与4至5月份的收入的变化率相同
D前6个月的平均收入为40万元
（注：结余=收入-支出）
正确答案
解析
读图可知A、B、C均正确，对于D，前6 个月的平均收入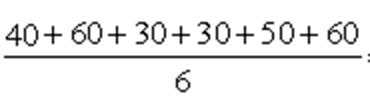
故选D。
考查方向
解题思路
读图可知A、B、C均正确。对于D，可通过计算再行确认。
易错点
本题易看错题目中“错误”二字导致选错。
知识点
9.某市今年1月份前30天空气质量指数（AQI）的趋势图如图:
当空气质量指数（AQI）小于100时,表示空气质量优良.某人随机选择当月1日至10日中的某一天到达该市,并停留2天,若以空气质量优良的频率作为概率,则此人停留期间空气质量2天都是优良的概率为___________.
正确答案
解析
利用频率=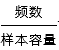
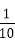
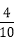
知识点
5．为了了解居民家庭网上购物消费情况，某地区调查了10000户家庭的月消费金额（单位：元），所有数据均在区间
正确答案
750
解析
由题意得，被调查的10000户家庭中，消费额在1000元以下的户数有：（0.0001+0.00015）×500×10000=750户．
考查方向
本题主要考查统计的概念，直方图．考查概念的理解和运算能力，难度较小.
解题思路
本题主要考查统计的概念，直方图等知识。
解题步骤如下：找出前面二个矩形的高度，即纵坐标、利用公式求得结果。
易错点
本题易错点是看不懂直方图中矩形面积的意义，把1000元以下，理解为包含1000元。
知识点
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
某车间共有
（1）根据茎叶图计算样本均值；
（2）日加工零件个数大于样本均值的工人为优秀工人，根据茎叶图推断该车间
（3）从该车间
正确答案
见解析
解析
(1)由题意可知,样本均值
(2)
(3)
而恰有1名优秀工人有
知识点
甲、乙两名运动员参加“选拔测试赛”， 在相同的条件下，两人5次测试的成绩（单位：分）记录如下：
甲 86 77 92 72 78
乙 78 82 88 82 95
（1）用茎叶图表示这两组数据；
（2）现要从甲乙二人中选派一名运动员参加比赛，你认为选派谁参赛更好？说明理由（不用计算）；
（3）若将频率视为概率，对运动员甲在今后三次测试成绩进行预测，记这三次成绩高于
正确答案
见解析
解析
（1）茎叶图
————3分
（2）由图可知，乙的平均成绩大于甲的平均成绩，且乙的方差小于甲的方差，且乙的最高分高于甲的最高分，因此应选派乙参赛更好，
————6分
（3）记甲“高于80分”为事件A，
分布列为：
————11分
知识点
为了解甲、乙两个班级某次考试的数学成绩（单位：分），从甲、乙两个班级中分别随机抽取
（1）从甲班的样本中有放回的随机抽取
（2）从甲、乙两个班级的样本中分别抽取
正确答案
见解析。
解析
（1）设事件
（2）
∴
知识点
根据某固定测速点测得的某时段内过往的100辆机动车的行驶速度(单位：km/h)绘制的频率分布直方图如图(3)所示，该路段限速标志牌提示机动车辆正常行驶速度为60 km/h~120 km/h，则该时段内过往的这100辆机动车中属非正常行驶的有 辆，图中的x值为 。
正确答案
15、0.0175；
解析
由直方图可知，这100辆机动车中属非正常行驶的有
知识点
如图，茎叶图表示甲、乙两名篮球运动员在五场比赛中的得分，其中一个数字被污损，则甲的平均得分不超过乙的平均得分的概率为 。
正确答案
7/10
解析
略
知识点
如图是7位评委给某作品打出的分数的茎叶图，那么这组数据的方差是 。
正确答案
解析
由茎叶图知，七个数据为88，89，89，90，91，91，92，
平均数为 
方差为 
知识点
扫码查看完整答案与解析