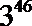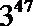- 诱导公式的推导
- 共118题
1
题型:
单选题
|
1. 集合


正确答案
A
解析
解析已在路上飞奔,马上就到!
知识点
诱导公式的推导
1
题型:简答题
|
16.将3封不同的信投进A、B、C、D这4个不同的信箱、假设每封信投入每个信箱的可能性相等.
(Ⅰ)求这3封信分别被投进3个信箱的概率;
(Ⅱ)求恰有2个信箱没有信的概率;
(Ⅲ)求A信箱中的信封数量的分布列和数学期望.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
诱导公式的推导
1
题型:
单选题
|
10.对于三次函数f(x)=ax3+bx2+cx+d(a










正确答案
B
解析
解析已在路上飞奔,马上就到!
知识点
诱导公式的推导
1
题型:简答题
|
19.某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响. 已知某学生只选修甲的概率为



(1)记“函数



(2)求
正确答案
解:(1)设该学生选修甲、乙、丙的概率分别为

依题意得
若函数


当
∴事件

(2)依题意知
则
∴

解析
解析已在路上飞奔,马上就到!
知识点
诱导公式的推导
1
题型:
单选题
|
10.将数列
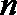
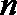
正确答案
B
解析
解析已在路上飞奔,马上就到!
知识点
诱导公式的推导
下一知识点 : 诱导公式的作用
扫码查看完整答案与解析