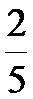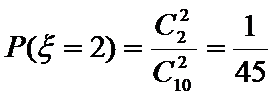- 频率分布直方图
- 共93题
11. 某调查机构调查了某地100个新生婴儿的体重,并根据所得数据画出了样本的频率分布直方图(如图所示),则新生婴儿的体重(单位:kg)在[3.2,4.0)的人数是__________。
正确答案
40
解析
解析已在路上飞奔,马上就到!
知识点
5.如图所示的茎叶图记录了某运动员在某赛季一些场次的得分,则该运动员的平均得分为( )
正确答案
18
解析
解析已在路上飞奔,马上就到!
知识点
4.某地气象局把2015年11月的每一天的最低气温作了统计,并绘制了如图所示的频率分布直方图,假设该月温度的中位数为me,众数为m0,平均数为
正确答案
解析
从表中看出,温度值的众数m0=5.由频率分布直方图,知30天最低温度值分布为3度(2天),4度(3天),5度(10天),6度(6天),7度(3天),8度(2天),9度(2天),10度(2天),则中位数me=



知识点
17.某班同学参加社会实践活动,对本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如右(部分有缺损):
(1)补全频率分布直方图(需写出计算过程);
(2)现从[40,55)岁年龄段样本中采用分层抽样方法抽取6人分成A、B两个小组(每组3人)参加户外体验活动,记A组中年龄在[40,45)岁的人数为


正确答案
(1)0.06;
(2)
解析
本题属于概率统计中的基本问题,题目的难度是逐渐由易到难
(1)因为第二组的频率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3所以高为0.3/5=0.06。频率直方图如下:
(2)因为[40,45)组、[45,50)组和[50,55)组的人数比为0.03:0.02:0.01=3:2:1,所以三组中应抽出的人数分别为3、2、1.




考查方向
本题考查了概率统计中的频率分布直方图和离散型随机变量的分布列和数学期望的问题.属于高考中的高频考点。
解题思路
无
易错点
1、第一问中的高为频率/组距。
2、第二问中随机变量的取值集对应的概率。
知识点
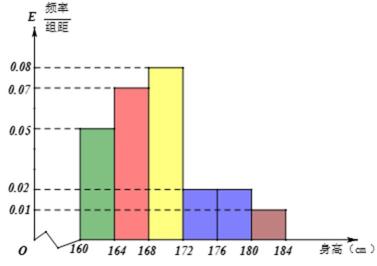
18.某市一次全市高中男生身高统计调查数据显示:全市100 000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160 cm和184 cm之间,将测量结果按如下方式分成6组:第一组 [160,164],第二组[164,168],…,第6组[180,184],下图是按上述分组方法得到的频率分布直方图.
(Ⅰ)试评估该校高三年级男生在全市高中男生中的平均身高状况;
(Ⅱ)求这50名男生身高在172 cm以上(含172 cm)的人数;
(Ⅲ)在这50名男生身高在172 cm以上(含172 cm)的人中任意抽取2人,该2人中身高排名(从高到低)在全市前130名的人数记为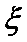
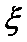
参考数据:若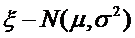
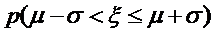
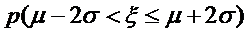
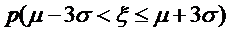
正确答案
(Ⅰ)平均值168.72,高于全市平均值
(Ⅱ)10人.
(Ⅲ)
解析
(Ⅰ)由直方图,经过计算该校高三年级男生平均身高为
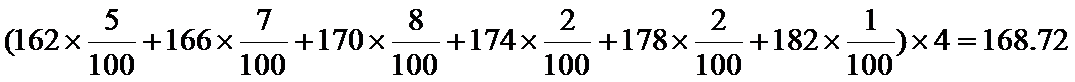
高于全市的平均值168(或者:经过计算该校高三年级男生平均身高为168.72,比较接近全市的平均值168).
(Ⅱ)由频率分布直方图知,后三组频率为(0.02+0.02+0.01)×4=0.2,人数为0.2×50=10,即这50名男生身高在172 cm以上(含172 cm)的人数为10人.
(Ⅲ)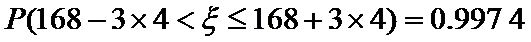
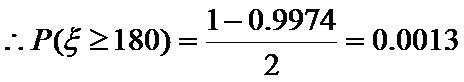
所以,全市前130名的身高在180 cm以上,这50人中180 cm以上的有2人.
随机变量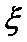
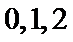
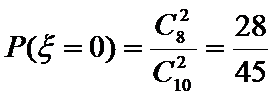
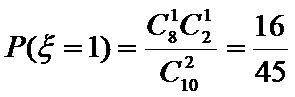
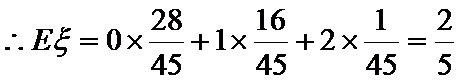
考查方向
解题思路
第一问估算,直接用每组的平均值乘以频率,然后相加即得
第二问先计算后三组的频率和,然后乘以总人数即得
第三问先根据正态分布概率计算出全市前130名是在那个身高区间,然后再计算50个人中有几个在这个区间,最后根据组合数计算出各变量的期望值,再相加即得。
易错点
1、对频率分布直方图认识不清,误把纵坐标当概率
2、对正态分布的意义理解不正确,不能正确计算概率
知识点
扫码查看完整答案与解析