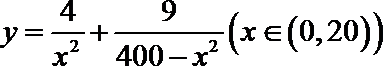• 职业资格类
  • 建筑类
  • 学历类
  • 财会类
  • 医药类
  • 全部考试
职业资格类
建筑类
学历类
财会类
计算机类
公务员
医药类
  • 函数解析式的求解及常用方法
  • 共177题
  • 函数解析式的求解及常用方法
  • 共177题

热门试卷

X 查看更多试卷
1
题型：简答题
|
简答题 · 14 分

21.已知函数，一部分图像如图，若.

（Ⅰ）求解析式；

（Ⅱ）当时，求证；

（Ⅲ）若，问是否存在实数和正整数，使在内恰有个零点，若存在，求值，若不存在，说明理由.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法
1
题型： 单选题
|
单选题 · 5 分

11.化极坐标方程为直角坐标方程为（    ）

A

B

C

D

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法
1
题型：填空题
|
填空题 · 5 分

14.在直角坐标系中圆C的参数方程为（为参数），若以原点为极点，以轴正半轴为极轴建立极坐标系，则圆的极坐标方程为（      ）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法
1
题型： 单选题
|
单选题 · 5 分

8．某商场五一前30天电脑销售总量与时间的关系大致满足，则该商场用t天平均售出（如前5天的平均售出为）的电脑最少为（    ）

A18

B27

C20

D16

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法
1
题型： 单选题
|
单选题 · 5 分

6． 为了得到函数的图象，只需将函数的图象（    ）

A向左平移个长度单位

B向右平移个长度单位

C向左平移个长度单位

D向右平移个长度单位

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法
1
题型：填空题
|
填空题 · 5 分

13．的展开式中项的系数等于（         ） 。（用数学作答）

正确答案

6

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法
1
题型：简答题
|
简答题 · 16 分

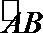
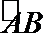
21．两城市A和B相距20km，现计划在两城市外以AB为直径的半圆弧上选择一点C建造垃圾处理厂，其对城市的影响度与所选地点到城市的距离有关，对城A和城B的总影响度为城A与城B的影响度之和，记C点到城A的距离为x km，建在C处的垃圾处理厂对城A和城B的总影响度为y，统计调查表明：垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比，比例系数为4；对城B的影响度与所选地点到城B的距离的平方成反比，比例系数为k，当垃圾处理厂建在的中点时，对城A和城B的总影响度为0．065

　　

（1）将y表示成x的函数；

（2）判断弧上是否存在一点，使建在此处的垃圾处理厂对城A和城B的总影响度最小？若存在，求出该点到城A的距离；若不存在，说明理由

正确答案

（1）由题意得，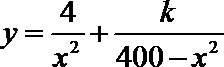

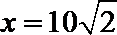
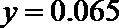
又∵当时，，

∴

∴

（2），

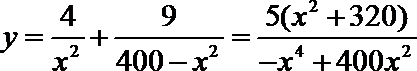
令，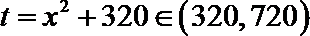

则，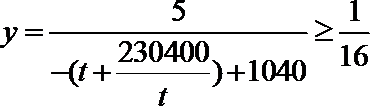

当且仅当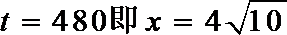时，等号成立． 

∴弧AB上存在一点，该点到城A的距离为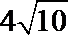时，使建在此处的垃圾处理厂对城A和城B的总影响度最小为0.0625

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法函数模型的选择与应用基本不等式的实际应用
1
题型：简答题
|
简答题 · 12 分

18.已知箱中装有4个白球和5个黑球，且规定：取出一个白球得2分，取出一个黑球得1分．现从该箱中任取3个球(无放回，且每球取到的机会均等)，记随机变量X为取出3球所得分数之和．

（Ⅰ）求X的分布列；

（Ⅱ）求X的数学期望E(X)．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法
1
题型： 单选题
|
单选题 · 4 分

17．设直线与球有且只有一个公共点，从直线出发的两个半平面、截球的两个截面圆的半径分别为和，二面角的平面角为，则球的表面积为  （    ）

A

B

C

D

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法
1
题型：简答题
|
简答题 · 14 分

19．如图：某污水处理厂要在一个矩形污水处理池的池底水平铺设污水净化管道，是直角顶点）来处理污水，管道越短，铺设管道的成本越低．设计要求管道的接口是的中点，分别落在线段上。已知米，米，记。

（1）试将污水净化管道的长度表示为的函数，并写出定义域；

（2）若，求此时管道的长度；

（3）问：当取何值时，铺设管道的成本最低？并求出此时管道的长度。

正确答案

（1），，

由于，，，。

所以 ，

（2）时，，；

（3）=，设，

则，由于，

所以 ，

在 内单调递减，

于是当时． 的最小值米

答：当时，所铺设管道的成本最低，此时管道的长度为米

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法
继续学习 学习下一知识点
下一知识点 : 区间与无穷的概念
百度题库 > 高考 > 理科数学 > 函数解析式的求解及常用方法

扫码查看完整答案与解析

  • 上一题
  • 1/10
  • 下一题