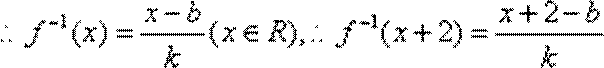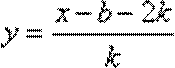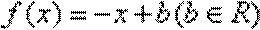- 函数解析式的求解及常用方法
- 共177题
21.已知


(1)求
(2)是否存在实数a,使得当
正确答案
(1)设

故函数
(2)假设存在实数a,使得当

①当
由于



②当

综上所知,存在实数

解析
解析已在路上飞奔,马上就到!
知识点
13.设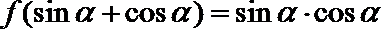
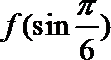
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数

(Ⅰ)求函数
(Ⅱ)设











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22. 抛物线








(1)用

(2) 比较
(3)若


正确答案
(1)由抛物线经过点


又抛物线过点


所以
(2)




故

又

(3)设切点
又
所以切线的方程是
又切线过原点,故
所以


两条切线的斜率为

由



所以
又两条切线垂直,故


所以
解析
解析已在路上飞奔,马上就到!
知识点
16.函数f(x)=Asin(ωx-)+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设α∈(0,2π),f()=2,求α的值.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数

(1)当
(2)当
(3)当
(4)当
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知函数



正确答案
(-1,1)
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数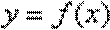


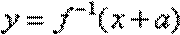
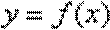
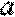
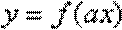


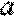
(1)判断函数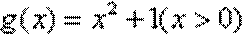
(2)求所有满足“2和性质”的一次函数;
(3)设函数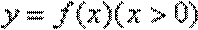
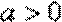
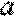

正确答案
(1)函数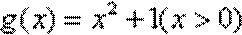
而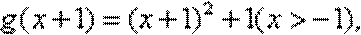
故函数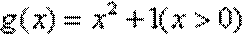
(2)设函数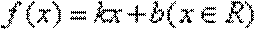
而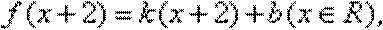
由“2和性质”定义可知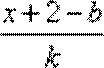

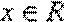
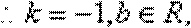
(3)设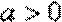

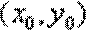
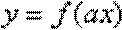
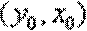

故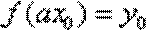
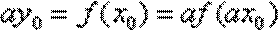
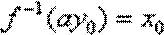
令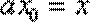

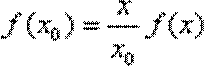
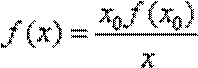
综上所述,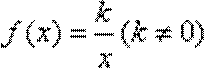
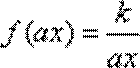
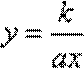
而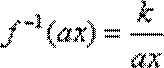


解析
解析已在路上飞奔,马上就到!
知识点
22.已知


(1)求
(2)是否存在实数


正确答案
(1)设

故函数
(2)假设存在实数

①当
由于



②当

综上所知,存在实数

解析
解析已在路上飞奔,马上就到!
知识点
21.如图,一吊灯的底是直径为












(1)将

(2)请你设计:当角


正确答案
(1)
(2)由(1)知,
令



当


∴当



解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析