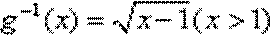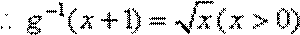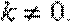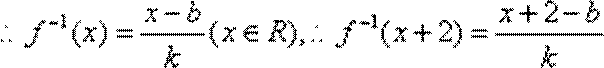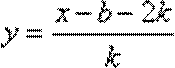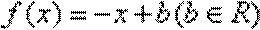- 函数解析式的求解及常用方法
- 共177题
21.已知


(1)求
(2)是否存在实数a,使得当
正确答案
(1)设

故函数
(2)假设存在实数a,使得当

①当
由于



②当

综上所知,存在实数

解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数

(1)当
(2)当
(3)当
(4)当
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知函数



正确答案
(-1,1)
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数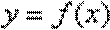


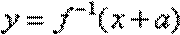
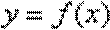
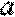
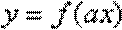


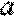
(1)判断函数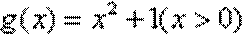
(2)求所有满足“2和性质”的一次函数;
(3)设函数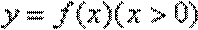
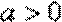
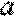

正确答案
(1)函数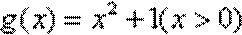
而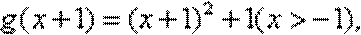
故函数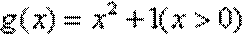
(2)设函数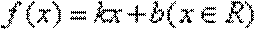
而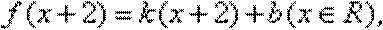
由“2和性质”定义可知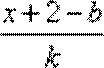

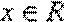
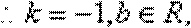
(3)设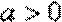

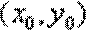
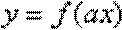
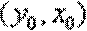

故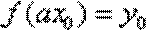
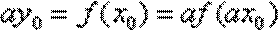
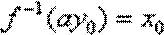
令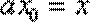

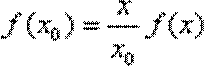
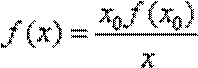
综上所述,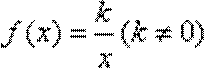
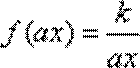
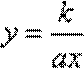
而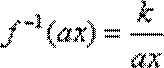


解析
解析已在路上飞奔,马上就到!
知识点
22.已知


(1)求
(2)是否存在实数


正确答案
(1)设

故函数
(2)假设存在实数

①当
由于



②当

综上所知,存在实数

解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析