• 职业资格类
  • 建筑类
  • 学历类
  • 财会类
  • 医药类
  • 全部考试
职业资格类
建筑类
学历类
财会类
计算机类
公务员
医药类
  • 函数解析式的求解及常用方法
  • 共177题
  • 函数解析式的求解及常用方法
  • 共177题

热门试卷

X 查看更多试卷
1
题型： 单选题
|
单选题 · 5 分

10.如图，长方形ABCD的边AB=2，BC=1，O是AB的中点，点P沿着BC，CD.DA运动，∠BOP=x。将动点P到AB两点距离之和表示为x的函数f（x），则f（x）

的图像大致为(  )

AA.

BB.

CC.

DD.

正确答案

B

知识点

函数解析式的求解及常用方法知图选式与知式选图
1
题型： 单选题
|
单选题 · 5 分

5. 函数的值域是（   ）

A

B

C

D

正确答案

D

解析

令，则t>0,则原函数变为，在t>0可以求出其范围是。

考查方向

函数的值域。

解题思路

可以用换元法解。

易错点

粗心计算出错。

知识点

函数解析式的求解及常用方法
1
题型：简答题
|
简答题 · 12 分

已知函数（其中为常数且）在处取得极值．

24.当时，求的极大值点和极小值点；

25.若在上的最大值为1，求的值．

第(1)小题正确答案及相关解析

正确答案

略

第(2)小题正确答案及相关解析

正确答案

略

1
题型：填空题
|
填空题 · 4 分

5．若函数的图像与对数函数的图像关于直线对称，则的解析式为_____________．

正确答案

解析

∵函数的与函数的图像关于直线对称

∴以、代替原来中的、，得

∴所求解析式为．

考查方向

本题考查函数的图像变换，是容易题．

解题思路

函数的与函数的图像关于直线对称，故以、代替原来中的、，化简得到关于的函数即可．

易错点

混淆各种函数图像变换．

知识点

函数解析式的求解及常用方法指数函数与对数函数的关系反函数
1
题型： 单选题
|
单选题 · 5 分

10.如图所示的阴影部分是由底边长为，高为的等腰三角形及宽为，长分别为和的两矩形所构成.设函数是图中阴影部分介于平行线及之间的那一部分的面积，则函数的图象大致为 

 

A

B

C

D

正确答案

C

解析

当时，；

当时，；

当时，；

当时，；

由的解析式得知C正确。

考查方向

本题主要考查求分段函数的解析式以及识别图像的能力。

解题思路

1、先求当时，的解析式；

2. 接着求当a在其他段时，的解析式，然后根据解析式选出正确选项。

易错点

当时的解析式求错导致结果出错。

知识点

函数解析式的求解及常用方法知图选式与知式选图
1
题型：简答题
|
单选题

在一定职业活动中应遵循的、体现一定职业特征的、调整一定职业关系的职业行为准则和规范是()。

A．狭义的职业道德
B．广义的职业道德
C．一半职业道德
D．会计职业道德

正确答案

A

解析

暂无解析

1
题型： 单选题
|
单选题 · 5 分

A

B

C

D

正确答案

B

知识点

函数解析式的求解及常用方法画函数的图象
1
题型：简答题
|
简答题 · 14 分

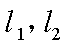
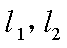
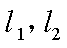
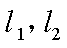
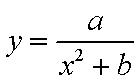
17.某山区外围有两条相互垂直的直线型公路，为进一步改善山区的交通现状，计划修建一条连接两条公路和山区边界的直线型公路，记两条相互垂直的公路为，山区边界曲线为C，计划修建的公路为l，如图所示，M，N为C的两个端点，测得点M到的距离分别为5千米和40千米，点N到的距离分别为20千米和2.5千米，以所在的直线分别为x，y轴，建立平面直角坐标系xOy，假设曲线C符合函数（其中a，b为常数）模型.

（1）求a，b的值；

（2）设公路l与曲线C相切于P点，P的横坐标为t.

①请写出公路l长度的函数解析式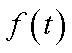，并写出其定义域；

②当t为何值时，公路l的长度最短？求出最短长度.

正确答案

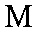
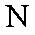
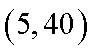
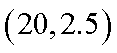
（1）由题意知，点，的坐标分别为，．

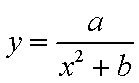
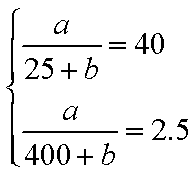
将其分别代入，得，

解得．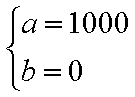

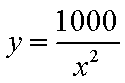
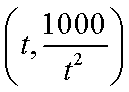
（2）①由（1）知，（），则点的坐标为，

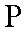
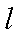
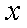
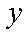
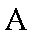
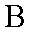
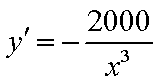
设在点处的切线交，轴分别于，点，，

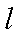
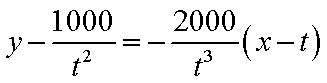
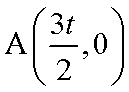
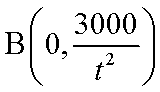
则的方程为，由此得，．

故，．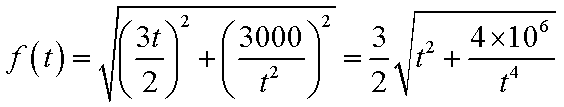

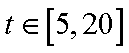
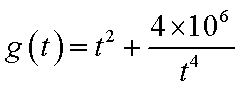
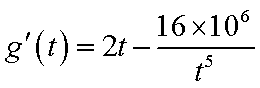
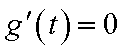
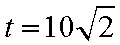
②设，则．令，解得．

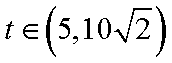
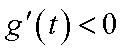
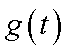
当时，，是减函数；

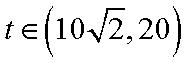
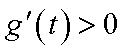
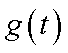
当时，，是增函数．

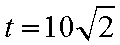
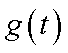
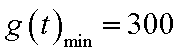
从而，当时，函数有极小值，也是最小值，所以，

此时．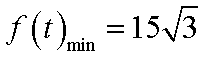

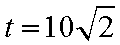
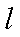
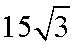
答：当时，公路的长度最短，最短长度为千米．

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法导数的几何意义导数的运算
1
题型： 单选题
|
单选题 · 5 分

10.如图，长方形的边，，是的中点，点沿着边，与运动，记.将动到、两点距离之和表示为的函数，则的图像大致为（    ）

A

B

C

D

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法知图选式与知式选图
1
题型：简答题
|
简答题 · 8 分

19. 某创业团队拟生产、两种产品，根据市场预测，产品的利润与投资额成正比（如图1），产品的利润与投资额的算术平方根成正比（如图2）；

（注：利润与投资额的单位均为万元）

（1）分别将、两种产品的利润、表示为投资额的函数；

（2）该团队已筹集到10万元资金，并打算全部投入A、B两种产品生产，问：当B产品的投资额为多少万元时，生产两种产品A、B能获得最大利润，最大利润为多少？

正确答案

，

解析

（1）由图易知，

（2）设B产品的投资额为万元，则A产品的投资额为万元。，，令，则可以得函数

，即，当，即时的最大值为

考查方向

实际问题中构造函数求最值问题。

解题思路

（1）图1所示的函数为正比例函数，图2 所示的函数为幂函数，直接代入点的坐标即可。

（2）由1的结论，我们设B产品的投资额为万元，则A产品的投资额为万元，这可以构造出一个关于收益的函数，然后利用求函数最大值的方法进行求解。

易错点

（1）函数图像的正确识别。

（2）①注意定义域②构造函数求最值要熟练。

知识点

函数解析式的求解及常用方法二次函数在闭区间上的最值
棒棒哒，已学完当前知识点 学习下一知识点
下一知识点 : 区间与无穷的概念
百度题库 > 高考 > 理科数学 > 函数解析式的求解及常用方法

扫码查看完整答案与解析

  • 上一题
  • 1/10
  • 下一题