- 函数解析式的求解及常用方法
- 共177题
1
题型:填空题
|
方程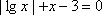
正确答案
1
解析
略
知识点
函数解析式的求解及常用方法
1
题型:
单选题
|
某个体企业的一个车间有8名工人,以往每人年薪为1万元,从今年起,计划每人的年薪都比上一年增加20%,另外,每年新招3名工人,每名新工人的第一年的年薪为8千元,第二年起与老工人的年薪相同,若以今年为第一年,如果将第n年企业付给工人的工资总额y(万元)表示成n的函数,则其表达式为
正确答案
A
解析
略
知识点
函数解析式的求解及常用方法
1
题型:简答题
|
函数







(1)求函数
(2)若

正确答案
见解析。
解析
(1)∵
由

∵

∴
(2)由

∵
∴
∴
∴

知识点
函数解析式的求解及常用方法
1
题型:填空题
|
设定义在R上的函数
①

③当


正确答案
解析
略
知识点
函数解析式的求解及常用方法
1
题型:简答题
|
已知函数
(1)当
(2)若函数
(3)若对任意给定的

正确答案
见解析。
解析
解析:(1)当
由
故
(2)因为
故要使函数

即对
令
则

综上,若函数

(3)
所以,函数
故
此时,当
即②对任意
由③式解得:
综合①④可知,当
在
使
知识点
函数解析式的求解及常用方法
下一知识点 : 区间与无穷的概念
扫码查看完整答案与解析



















