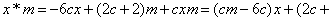- 函数解析式的求解及常用方法
- 共177题
对任意实数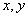
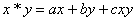
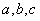
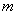
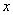
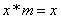
正确答案
解析
由定义可知,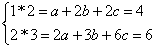
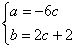
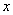
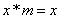
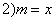
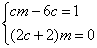
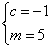
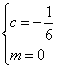
知识点
已知


正确答案
1
解析
二项展开式的通项为







知识点
已知函数

(1)求函数
(2)求函数

正确答案
见解析。
解析
(1)

因此,函数

(2)由题易知

在区间
又


所以,函数


知识点
设函数

(1)当





(2)若函数

正确答案
见解析。
解析
(1)由题易得

因为直线

则令



易得,







①当





②当

则

令

易得方程(*)在




所以直线

综上所述,直线


(2)由题易知,



即



即
设






所以
所以当

要使



综上所述,若


知识点
已知




(1)求
(2)设




正确答案
见解析
解析
(1)如图,在


可得
又 


则函数

其中定义域为
说明:亦可用积化和差方法化简:

(2)
由


1




2




因而存在实数


知识点
扫码查看完整答案与解析