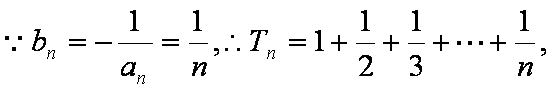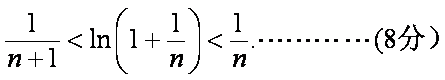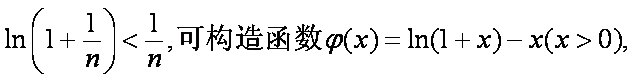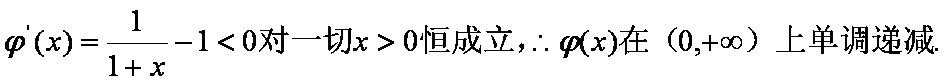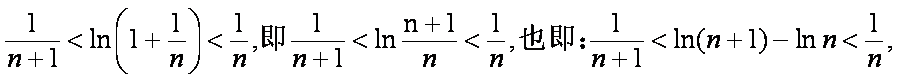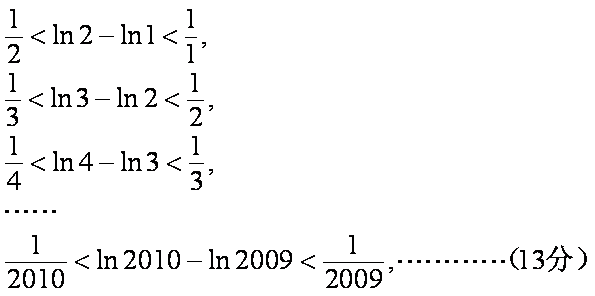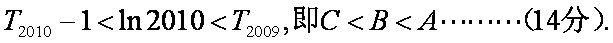- 函数解析式的求解及常用方法
- 共177题
设点P是曲线y=x2上的一个动点,曲线y=x2在点P处的切线为l,过点P且与直线l垂直的直线与曲线y=x2的另一交点为Q,则PQ的最小值为 。
正确答案
解析
设

所以过点P且与直线l垂直的直线方程为
联立y=x2得:
设Q(x1,y1),则


所以|PQ|=
=
=

令t=
g(t)=
则
当t∈(0,2)时,g′(t)<0,g(t)为减函数,
当t∈(2,+∞)时,g′(t)>0,g(t)为增函数,
所以
所以PQ的最小值为
知识点
在矩形ABCD中,|AB|=2



(1)求证:直线ER与GR′的交点P在椭圆


(2)若M、N为椭圆

正确答案
见解析
解析
解析:(1)∵


又


又


由①②得
∵
∴直线



(2)①当直线
不妨取

②当直线

联立方程
则

又
即
将
解得

∴直线过定点
∴


∴
由



∴


知识点
随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员






正确答案
解析
解析: 设裁员


依题意 



又140<

(1)当0<




(2)当




综上所述,当70<



知识点
对于函数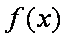
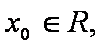
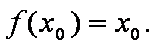
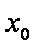
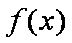
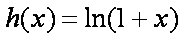

(1)试求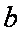
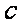
(2)若

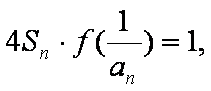
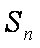
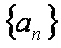
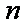
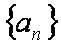
(3)设

正确答案
见解析
解析
(1)由
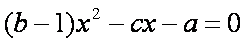
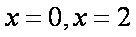
(2)若c=2,则b=2.
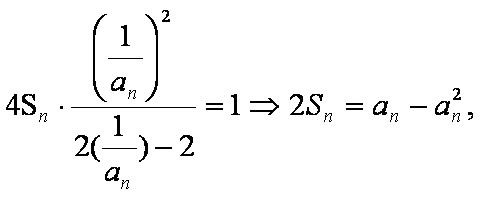
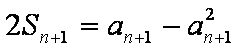
②式-①式可得:
当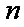
……………6分
故
(3)
以下首先证明不等式
事实上要证
则
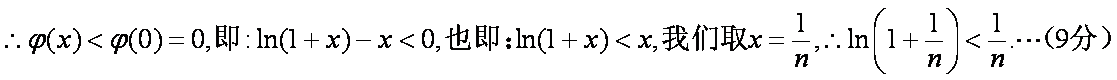
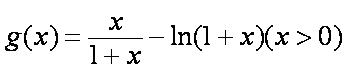
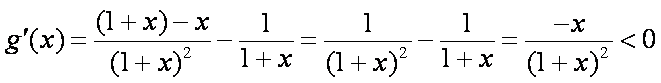
故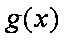
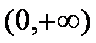
我们取
综上:
分别令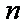
将这2009个式子累加得:
知识点
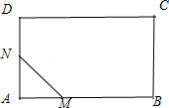
将一张长8cm,宽6cm的长方形的纸片沿着一条直线折叠,折痕(线段)将纸片分成两部分,面积分别为S1cm2,S2cm2,其中S1≤S2,记折痕长为lcm。
(1)若l=4,求S1的最大值;
(2)若S1:S2=1:2,求l的取值范围。
正确答案
见解析
解析
如图所示:不妨设纸片为长方形ABCD,AB=8cm,AD=6cm,其中点A在面积为S1的部分内,折痕有下列三种情形:
情形①情形②情形③
①折痕的端点M,N分别在边AB,AD上;
②折痕的端点M,N分别在边AB,CD上;
③折痕的端点M,N分别在边AD,BC上。
(1)在情形②③中,MN≥6,故当l=4时,折痕必定是情形①。
设AM=xcm,AN=ycm,则x2+y2=16。
因为x2+y2≥2xy,当且仅当x=y时取等号,
所以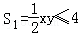
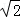
(2)由题意知,长方形的面积为S=6×8=48,
因为S1:S2=1:2,S1≤S2,所以S1=16,S2=32。
当折痕是情形①时,设AM=xcm,AN=ycm,则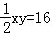
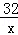
由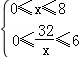
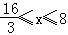
所以l=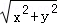
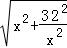
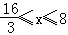
设f(x)=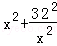
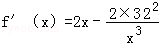
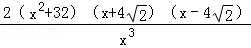
故当x∈(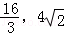
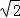
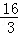
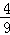
所以f(x)的取值范围为[64,80],从而l的范围是[8,4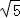
当折痕是情形②时,设AM=xcm,DN=ycm,则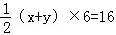
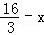
由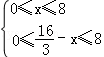
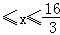
所以l=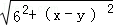
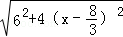
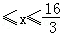
所以l的范围为[6,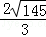
当折痕是情形③时,设BN=xcm,AM=ycm,则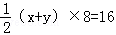
由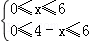
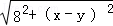
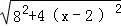
所以l的取值范围为[8,4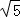
综上,l的取值范围为[6,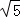
知识点
扫码查看完整答案与解析