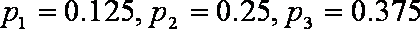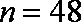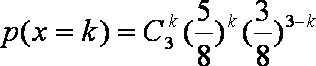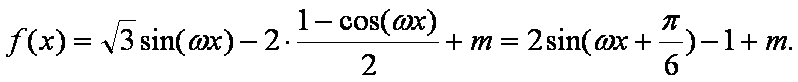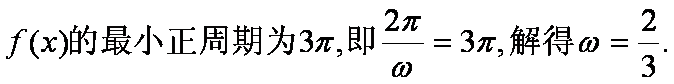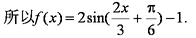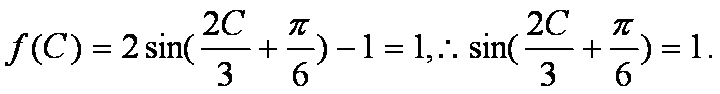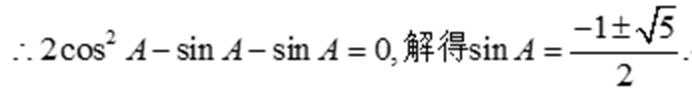- 函数解析式的求解及常用方法
- 共177题
已知函数f(x)=lnx+x2﹣ax。
(1)若函数f(x)在其定义域上是增函数,求实数a的取值范围;
(2)当a=3时,求出f(x)的极值:
(3)在(1)的条件下,若
正确答案
见解析
解析
(1)函数f(x)=lnx+x2﹣ax(x>0),则f′(x)=
∵函数f(x)在(0,+∞)上是单调增函数,
∴f′(x)≥0在(0,+∞)上恒成立,即
∴
∵当x>0时,



∴a的取值范围是(﹣∞,2
(2)当a=3时,
当0<x<
当
∴f(x)在(0,

∴f(x)极大值=f(

(3)设
∴g′(x)=
∵a∈(﹣∞,2
∴g′(x)>0
∴g(x)在(0,1)内为增函数
∴g(x)max=g(1)=2﹣a
∵
∴2﹣a≤0,解得a≥2。
知识点
已知函数


(1)求函数
(2)在




正确答案
见解析。
解析
(1)
又
∴
(2)
∴
解得


而
又

知识点
为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前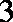
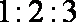
(1)求该校报考飞行员的总人数;
(2)以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中(人数很多)任选三人,设X表示体重超过60公斤的学生人数,求X的分布列和数学期望。
正确答案
见解析。
解析
(1)设报考飞行员的人数为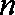
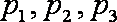
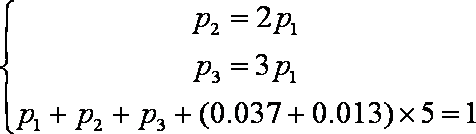
又因为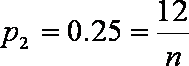
(2) 由(1)可得,一个报考学生体重超过60公斤的概率为
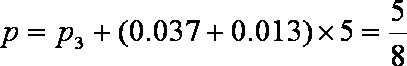
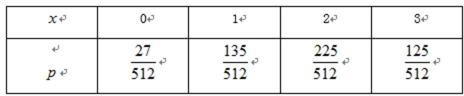
所以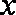

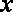
则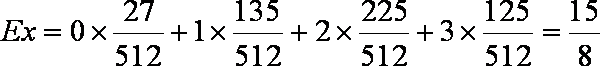
知识点
设函数
(1)当

(2)当

(3)若对任意



正确答案
见解析。
解析
(1)函数的定义域为
当



当




(2)



当




当



令
当



令


综上,当

当




当





(3)由(2)知,当


当




而




知识点
已知函数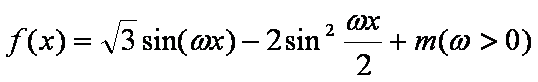
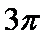
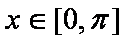
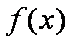
(1)求函数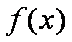
(2)在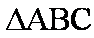
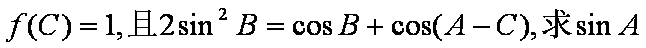
正确答案
见解析。
解析
(1)
依题意函数
所以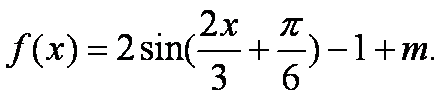
(2)
知识点
扫码查看完整答案与解析