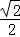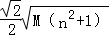- 导数的运算
- 共307题
函数

(1)当

(2)是否存在实数



(3)当


正确答案
见解析
解析
(1)明:设
则




(2)由

当


当


令


因为




所以

(3)由第一问得知

则
又


知识点
已知函数
(1)解不等式
(2)若

正确答案
见解析
解析
(1)f(x)+f(x+4)=|x-1|+|x+3|=
当x<-3时,由-2x-2≥8,解得x≤-5;
当-3≤x≤1时,f(x)≤8不成立;
当x>1时,由2x+2≥8,解得x≥3. …4分
所以不等式f(x)≤4的解集为{x|x≤-5,或x≥3}, …5分
(2)f(ab)>|a|f(),即|ab-1|>|a-b|, …6分
因为|a|<1,|b|<1,
所以|ab-1|2-|a-b|2
=(a2b2-2ab+1)-(a2-2ab+b2)
=(a2-1)(b2-1)>0,
所以|ab-1|>|a-b|,故所证不等式成立, …………10分
知识点
已知函数

(1)求函数f(x)的解析式;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c.若f(B)=1,


正确答案
见解析。
解析
(1)
由


(2)由
由
∴
由

再由余弦定理得,
知识点
已知函数
(1)求函数
(2)求函数
正确答案
见解析。
解析
(1)
则
最小正周期是
(2)

函数

知识点
设Sn是各项均为非零实数的数列{an}的前n项和,给出如下两个命题上:命题p:{an}是等差数列;命题q:等式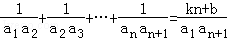
(1)若p是q的充分条件,求k,b的值;
(2)对于(1)中的k与b,问p是否为q的必要条件,请说明理由;
(3)若p为真命题,对于给定的正整数n(n>1)和正数M,数列{an}满足条件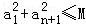
正确答案
见解析。
解析
(1)设{an}的公差为d,则原等式可化为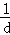
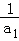
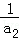
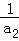
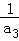
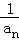
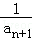
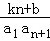
所以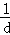
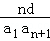
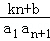
即(k﹣1)n+b=0对于n∈N*恒成立,所以k=1,b=0
(2)当k=1,b=0时,假设p是q的必要条件,即“若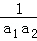
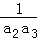
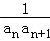
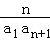
当n=1时,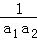
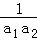
当n≥2时,若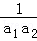
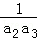
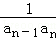
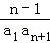
由①﹣②得,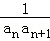
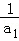


当n=2时,a1+a3=2a2,即a1、a2、a3成等差数列,
当n≥3时,(n﹣1)an﹣1﹣(n﹣2)an=a1④,即2an=an﹣1+an+1,所以{an}为等差数列,即p是q的必要条件,
(3)由

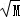
设{an}的公差为d,则an+1﹣a1=nd=rsinθ﹣rcosθ,
所以d=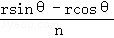
所以an=rsinθ﹣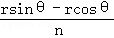
Sn=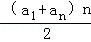
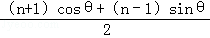
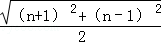
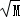
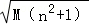
所以Sn的最大值为
知识点
扫码查看完整答案与解析