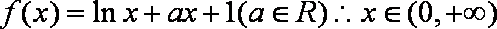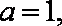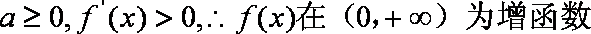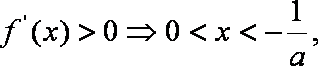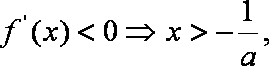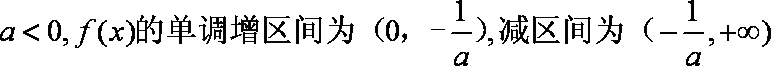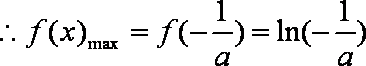- 导数的运算
- 共307题
已知数列

(1)求数列
(2)设

正确答案
见解析。
解析
(1)由题意得
∴

当

当
∴数列


(2)∵
∴

②—①得

知识点
已知直四棱柱


(1)求证:
(2)设F为AD中点,G为棱
求证:FG∥平面BDE。
正确答案
见解析
解析
(1)连接



∴

∴
(2)
过点




∴




四边形
∴


∴
知识点
若数列




正确答案
解析
由已知得

知识点
设数列





(1)求数列
(2)若





正确答案
见解析。
解析
(1)由




当



所以



(2)数列


从而


知识点
已知函数
(1)若直线

(2)证明曲线

(3)设


正确答案
见解析
解析
(1)
设切点为

代入

(2)令


又
所以


(3)
又因为




又当


则有


知识点
已知直线







(1)求椭圆的离心率;
(2)设椭圆左焦点为

正确答案
见解析
解析
设

(1)由


由

∴

∴点

又点


∴


(2)由(1)知

∴

由已知知
代入得


综上得
又


知识点
已知偶函数



正确答案
解析







由





知识点
已知函数


(1)求k的值;
(2)求
(3)设



正确答案
见解析
解析
解析:(1)
由已知,

(2)由(1)知,
设



由



当


综上可知,


(3)由(2)可知,当




当



设


当



所以当


所以
综上,对任意

知识点
今年我校高二文科班学生共有800人参加了数学与地理的学业水平测试,现学校决定利用随机数表法从中抽取100人进行成绩抽样统计,先将800人按001,002,。。。。。800进行编号:
(1)如果从第8行第7列的数开始向右读,请你依次写出最先检测的三个人的编号:(下面摘取了第7行至第9行)
(2)抽出100人的数学与地理的水平测试成绩如下表:
成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩良好的共有20+18+4=42人,若在该样本中,数学成绩优秀率是30%,求a、b的值;
(3)在地理成绩为及格的学生中,已知
正确答案
见解析
解析
(1)依题意,最先检测的3个人的编号依次为785,667,199; …………3分
(2)由

∵
∴
(3)由题意,知

∴满足条件的
且每组出现的可能性相同. ….…9分
其中数学成绩为优秀的人数比及格的人数少有:
(10,21),(11,20),(12,19),(13,18),(14,17),(15,16)共6组. …………11分
∴数学成绩为优秀的人数比及格的人数少的概率为
知识点
已知函数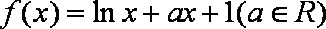
(1)若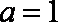
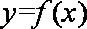
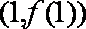
(2)求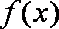
(3)设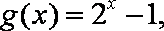
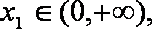
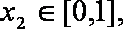
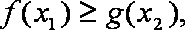
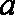
正确答案
见解析
解析
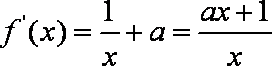
(1)当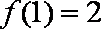
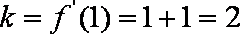
故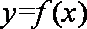
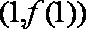
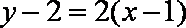
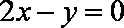
(2)当
当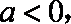
综上:
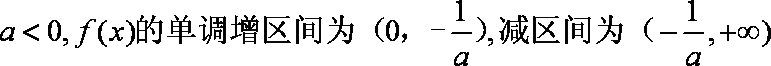
(3)由(2)知,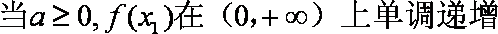
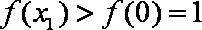
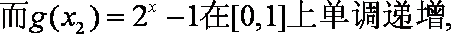
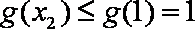
因此,当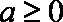
当
由题意知,只需满足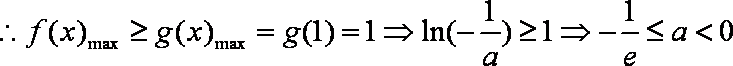
综上: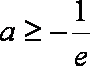
知识点
扫码查看完整答案与解析