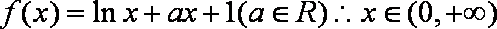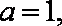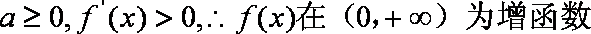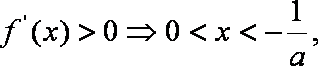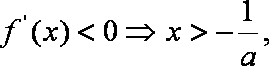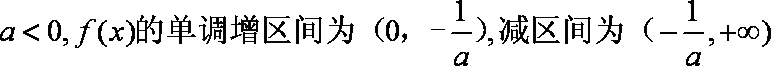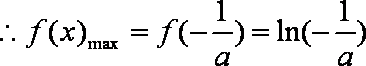- 导数的运算
- 共307题
已知直四棱柱


(1)求证:
(2)设F为AD中点,G为棱
求证:FG∥平面BDE。
正确答案
见解析
解析
(1)连接



∴

∴
(2)
过点




∴




四边形
∴


∴
知识点
已知直线







(1)求椭圆的离心率;
(2)设椭圆左焦点为

正确答案
见解析
解析
设

(1)由


由

∴

∴点

又点


∴


(2)由(1)知

∴

由已知知
代入得


综上得
又


知识点
已知偶函数



正确答案
解析







由





知识点
已知函数


(1)求k的值;
(2)求
(3)设



正确答案
见解析
解析
解析:(1)
由已知,

(2)由(1)知,
设



由



当


综上可知,


(3)由(2)可知,当




当



设


当



所以当


所以
综上,对任意

知识点
已知函数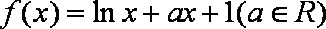
(1)若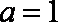
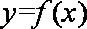
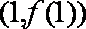
(2)求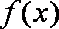
(3)设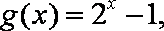
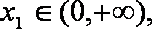
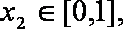
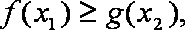
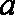
正确答案
见解析
解析
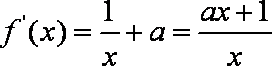
(1)当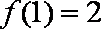
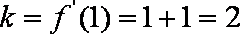
故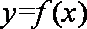
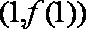
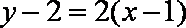
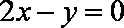
(2)当
当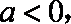
综上:
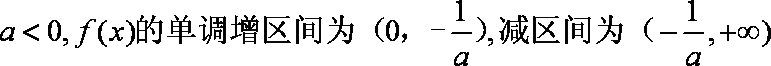
(3)由(2)知,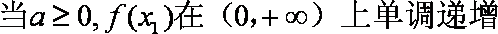
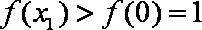
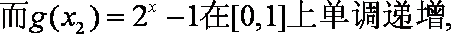
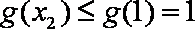
因此,当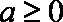
当
由题意知,只需满足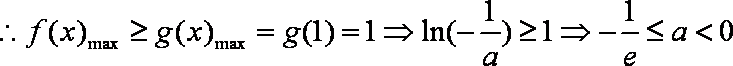
综上: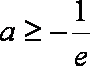
知识点
扫码查看完整答案与解析