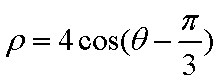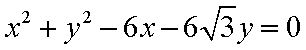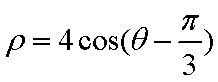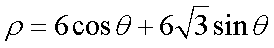- 导数的运算
- 共307题
设函数
(1)当

(2)若不等式


正确答案
见解析
解析
(1)当
根据图易得
(2)令
由


任意
由(1)知

故实数a的取值范围为
法(2) 易




知识点
设函数





正确答案
解析
略
知识点
已知:
正确答案
解析
由


知识点
函数



正确答案
解析
因为函数的最大值为1,最小值为











知识点
在极坐标系中, O为极点, 半径为2的圆C的圆心的极坐标为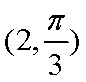
(1)求圆C的极坐标方程;
(2)
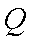
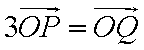
正确答案
(1)
(2)
解析
(1)设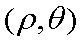
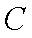
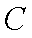
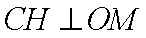
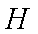
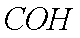
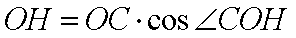
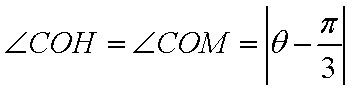
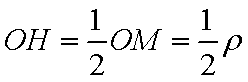
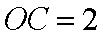
所以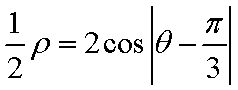
为所求的圆
(2)设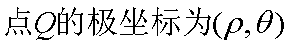
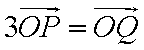
所以
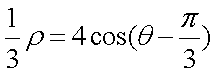
∴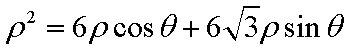
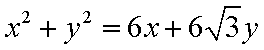
∴点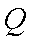
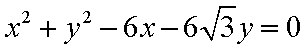
知识点
为了解某校高三毕业生报考体育专业学生的体重(单位:千克),将他们的体重数据整理后得到如下频率分布直方图.已知图中从左到右前3个小组的频率之比为
(1)求该校报考体育专业学生的总人数n;
(2)已知A、a是该校报考体育专业的两名学生,A的体重小于55千克, a的体重不小于




正确答案
见解析
解析
(1)由图知第四组的频率为
第五组的频率为.
又有条件知前三组的频率分别为
(2)易知按分层抽样抽取6名体重小于55千克和不小于70千克的学生中,体重小于55千克的学生4人,记为
从中抽取满足条件的所有结果有:

所求事件的概率为
知识点
在平面直角坐标系xOy中,已知圆O:x2+y2=4,直线l:12x﹣5y+c=0(其中c为常数),下列有关直线l与圆O的命题:
①当c=0时,圆O上有四个不同点到直线l的距离为1;
②若圆O上有四个不同点到直线l的距离为1,则﹣13<c<13;
③若圆O上恰有三个不同点到直线l的距离为1,则c=13;
④若圆O上恰有两个不同点到直线l的距离为1,则13<c<39;
⑤当c=±39时,圆O上只有一个点到直线l的距离为1。
其中正确命题的有 _________ (填上你认为正确的所有命题的序号)
正确答案
①②⑤
解析
圆心
















知识点
在△ABC中,a,b,c分别为内角A,B,C的对边,2asinA=(2b+c)sinB+(2c+b)sinC。
(1)求角A的大小
(2)求函数f(x)=cos2x﹣4cosAsinx(x∈R)的值域。
正确答案
见解析。
解析
(1)由已知,根据正弦定理得
即
故 


(2)由(1)知
因为




当

所以所求函数

知识点
已知全集


正确答案
解析


知识点
已知函数

正确答案
解析
当








知识点
扫码查看完整答案与解析