- 导数的运算
- 共307题
已知函数


(1)求实数a、b的值;
(2)求函数f(x)在区间[-1,2]上的最大值;
(3)曲线y=f(x)上存在两点M、N,使得△
正确答案
(1)a=1,b=0
(2)c·ln2
(3)(0,+∞)
解析
(1)当

因为函数图像在点

所以切点坐标为
解得
(2)由(1)得,当

令






对于


当

当


此时


当



令





当



综上可知,当



当



(3)


不妨设


若

由

即
即
若




所以



即

由于函数

实数

知识点
如图,在△






(1)求证:
(2)当


正确答案
见解析。
解析
(1)连结











从而
(2)由条件得


所以



知识点
设各项均为正数的数列




(1)证明:
(2)求数列
(3)证明:对一切正整数
正确答案
见解析
解析
(1)证明:当

又
(2)解:
















(3)证明:
知识点
设函数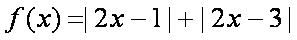
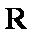
(1)解不等式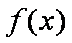
(2)若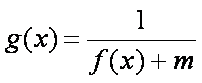
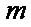
正确答案
(1)
(2)m>-2
解析
(1)原不等式等价于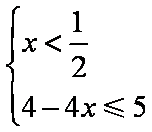
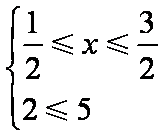
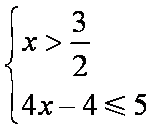
因此不等式的解集为
(2)由于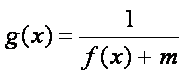
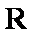
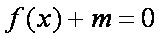
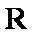
又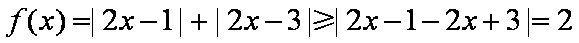
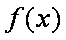
所以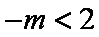
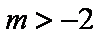
知识点
已知直三棱柱





(1)求证:

(2)求三棱锥
正确答案
见解析。
解析
(1)证明:连结













(2)因为





知识点
为了解某班学生喜爱打篮球是否与性别有关,对该班50人进行问卷调查后得到了如下的列联表
已知在全部50人中随机抽取1人抽到喜爱篮球的学生的概率为0.6。
(1)请将上面的列联表补充完整;
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关系;
(3)已知喜爱打篮球的10位女生中,






正确答案
见解析。
解析
(1)因为喜爱篮球的学生数为

(2)由(1)可知
又
(3)从喜欢打羽毛球、喜欢乒乓球、喜欢踢足球的女生中各选出1名可以出现下面30种情形:






























其中






那么




知识点
现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽查了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表。
(1)由以上统计数据填下面2乘2列联表并问是否有99%的把握认为“月收入以5500为分界点对“楼市限购令” 的态度有差异;
(2)若对月收入在[15,25) ,[25,35)的被调查人中各随机选取1人进行追踪调查,求选中的2人中不赞成“楼市限购令”人数至多1人的概率。
正确答案
见解析
解析
解析:
(1)2乘2列联表

所以没有99%的把握认为月收入以5500为分界点对“楼市限购令”的态度有差异. …………6分
(2)从月收入在[15,25) ,[25,35)的被调查人中各随机选取1人,共有50种取法,
其中恰有两人都不赞成“楼市限购令”共有2种取法,所以至多1人不赞成“楼市限购令”共有48种方法,所以
知识点
已知双曲线

正确答案
解析
略
知识点
函数


正确答案
解析
由


则




知识点
在数列

(1)证明

(2)求

正确答案
见解析
解析
(1)



(2)

①-② 得:


知识点
扫码查看完整答案与解析