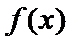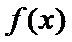- 导数的运算
- 共307题
8.设函数f(x)= 
正确答案
解析
易证得函数f(x)在[1,+∞)上单调递增.
当x<1时,得6-x2>1⇒-


当x≥1时,得6-x2>x⇒-3<x<2,则1≤x<2.
综上可得不等式的解集为(-
知识点
10.在R上定义运算*:a*b=2ab+2a+b,且f(x)= 
正确答案
解析
知识点
4.已知函数f(x)=2f'(1)ln x+x2,则f(x)=( )
正确答案
解析
f'(x)= 
得f'(1)=2f'(1)+2,解得f'(1)=-2.
所以f(x)=-4ln x+x2,故选A.
知识点
2.已知定义域为R的函数f(x)满足f(x)=2x+ax(a>0且a≠1),且f(x)的导函数满足f'(x)>2,则a的取值范围为( )
正确答案
解析
由f'(x)>2可知f'(x)-2>0,设F(x)=f(x)-2x,∴F'(x)>0,∴F(x)是R上的单调递增函数.又由f(x)=2x+ax可知f(x)-2x=ax,故a>1.
知识点
12.已知函数




正确答案
解析



考查方向
解题思路
根据函数的导函数恒大于等于零最后转化为求函数的最值问题。
易错点
1、不能通过函数的导函数来解决问题。
知识点
21

(I)若

(II)若当

(III)若
正确答案
(1)f(x)在(-∞,-1)和(0,+∞)上单调递增,在(-1,0)上单调递减;
(2)a≤1;(3)a=1
解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求;(2)要注意对参数的讨论.
(1)令f’(x)=ex-1+xex-x=(ex-1)(x+1)>0,得x<-1或x>0.
所以:f(x)在(-∞,-1)和(0,+∞)上单调递增,在(-1,0)上单调递减。
(2)f(x)=x(ex-1-ax),令g(x)= ex-1-ax,则g’(x)= ex-a.
若a≤1,则当x>0时g’(x)>0,g(x)为增函数,而g(0)=0,从而当x≥0时f(x)≥0;
若a>1,则当x∈(0,lna)时,g’(x)<0, g(x)为减函数,而g(0)=0,从而当x∈(0,lna)时,g(x)<0,即f(x)<0。
综上得a≤1.
(3)若f(x)无极值,则f(x)在R上单调。由f’(x)=(x+1)ex-1 -2ax,
若f(x)在R上单调递减,则f’(x)≤0,而利用不等式ex≥1+x,得f’(x)>0,与假设矛盾。
因此,f(x)在R上单调递增,即f’(x)≥0,显然f’(0)=0。
①当x>0时,2a≤

下面证明h(x)在(-∞,0)上单调递增:

当x>0时r’(x)>0,r(x)为增函数,r(x)>r(0)=0,h’(x)>0,h(x)在(0,+∞)上单调递增;
当x<0时r’(x)<0,r(x)为减函数,r(x)>r(0)=0,h’(x)>0,h(x)在(-∞,0)上单调递增;
当x>0时,由ex>1+x,得
得:2a≤2,a≤1。
②当x<0时,2a≥g(x),此时
得:2a≥2,a≥1。
综上得:a=1时f(x)无极值。
考查方向
本题考查了利用导数求含参数的函数极值,分类讨论,讨论点大体可以分成以下几类:
1、根据判别式讨论;
2、根据二次函数的根的大小;
3、定义域由限制时,根据定义域的隐含条件;
4、求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论;
5、多次求导求解等.
解题思路
本题考查导数的性质,解题步骤如下:
1、求导,然后解导数不等式,求单调区间。
2、对参数分类讨论求得零点个数。
易错点
第二问中的易丢对a的分类讨论。
知识点
12. 若函数

正确答案
解析
因为
所以
另
所以
所以可得


所以结合选项,b的取值范围为
考查方向
解题思路
先根据导函数在区间上有零点,得到b的取值范围,再利用b的取值范围,求出函数的单调区间,结合题目,选择正确的选项
易错点
判断b的取值范围,
知识点
21. 已知函数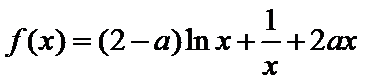
(Ⅰ)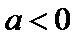
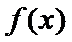
(Ⅱ)若对任意的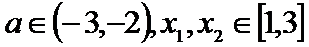
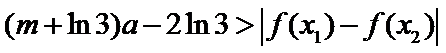
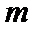
正确答案
(1)当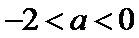
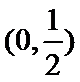
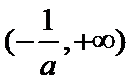
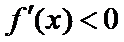

在区间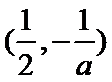
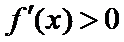
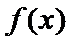
当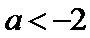
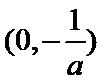
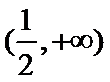
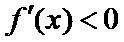
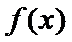
在区间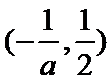
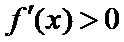
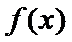
(2)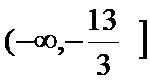
解析
试题分析:本题第(1)问属于用导数研究函数的性质的问题,是导数题目中的常见问题;第(2)问是用导数作为工具来解决不等式问题,题目综合性较强,难度较大。解答过程如下:
(Ⅰ) 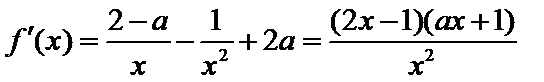
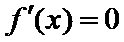
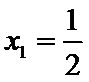
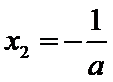
当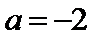
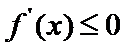
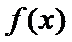
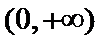
当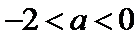
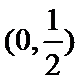
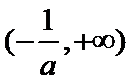
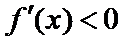

在区间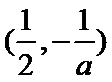
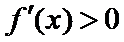
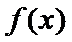
当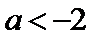
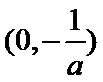
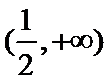
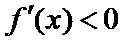
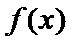
在区间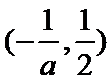
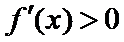
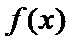
(Ⅱ)由(Ⅰ)知当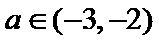
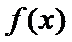
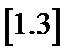
所以,当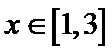
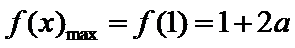
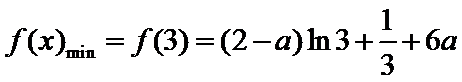
问题等价于:
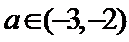
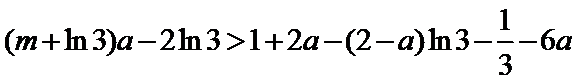
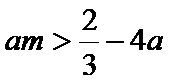
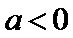
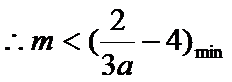
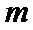
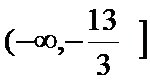
考查方向
解题思路
1、第(1)问可以通过函数的单调性与导数的关系,利用导数判断函数的单调性,在解题的过程中需要注意根据a的取值范围进行分类讨论;
2、第(2)问可以通过转化化归的方法,将问题转化为函数的最大、最小值问题进行求解。
易错点
解题的过程中忽略对a的取值范围进行分类讨论而导致错误。
知识点
12.已知函数


正确答案
解析
由函数











考查方向
解题思路
先要根据两个函数的图像上存在关于x轴对称的点这一信息建立关于a的关系,再利用导数求解。
易错点
本题容易因为不能准确判断两函数的图像存在关于x轴对称的点这一信息而导致不会做。
知识点
12.已知函数




正确答案
解析

当





当




得
当




综上可知
考查方向
解题思路
利用导数求解,首先求出导数,然后结合
易错点
本题容易因为不能对
知识点
扫码查看完整答案与解析