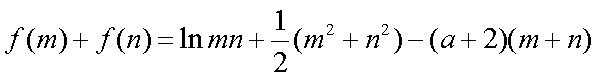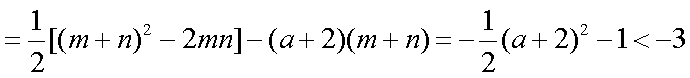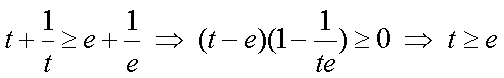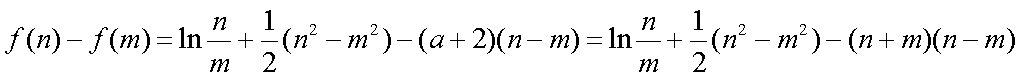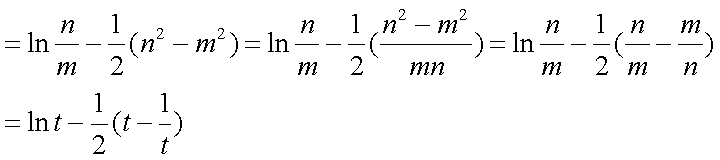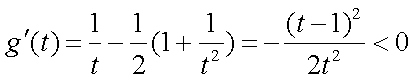- 导数的运算
- 共307题
已知函数
(1)试求b,c所满足的关系式;
(2)若b=0,方程
(3)若b=1,集合
正确答案
见解析
解析
(1)由
∴b、c所满足的关系式为
(2)由


方程


令


令


当


当





由函数



故所求


(3)由






当



当





当


注:可直接通过研究函数

知识点
已知


正确答案
解析


知识点
设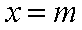
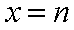
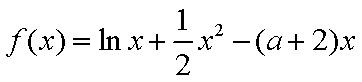
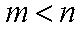
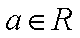
(1) 求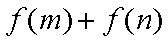
(2) 若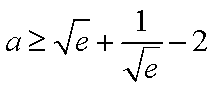
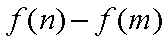
注:e是自然对数的底数。
正确答案
见解析
解析
(1)解:函数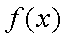
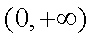
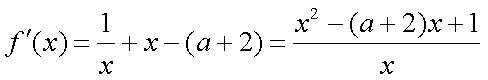
依题意,方程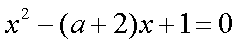
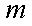
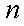
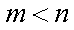
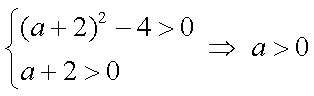
并且 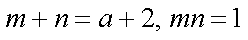
所以,
故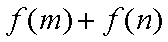
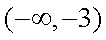
(2)解:当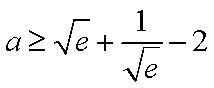
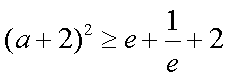
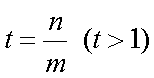
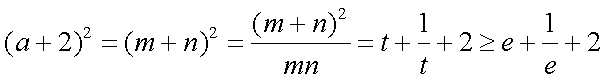
于是有
构造函数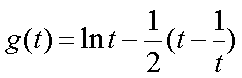
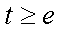

所以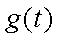
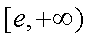
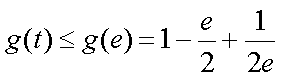
故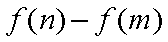
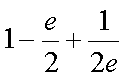
知识点
已知函数
(1)求函数
(2)令


正确答案
见解析
解析
(1)∵
∴

又

∴

故

(2)
定义域
则
设


由于



∴
又

由

∴只需
知识点
已知函数
(1)当


(2)当

正确答案
见解析。
解析
(1)当








(2)因为
所以

令
(Ⅰ)当

所以当



当



(Ⅱ)当

解得:
①若



②若






③ 当







综上所述:
当



当


当



知识点
扫码查看完整答案与解析