平面向量的基本定理及其意义
共28题

· 平面向量的基本定理及其意义

平面向量的基本定理及其意义
共28题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

已知点A(1，－1)，B(3,0)，C(2,1)，若平面区域D由所有满足＝λ＋μ(1≤λ≤2,0≤μ≤1)的点P组成，则D的面积为__________。

正确答案

解析

＝λ＋μ，＝(2,1)，＝(1,2)。

设P(x，y)，则＝(x－1，y＋1)。

∴得

∵1≤λ≤2,0≤μ≤1，

可得如图。

可得A1(3,0)，B1(4,2)，C1(6,3)，

|A1B1|＝，

两直线距离，

∴S＝|A1B1|·d＝3.

知识点

平面向量的基本定理及其意义向量在几何中的应用

题型：填空题

填空题 · 4 分

设e1，e2为单位向量，非零向量b＝xe1＋ye2，x，y∈R.若e1，e2的夹角为，则的最大值等于__________。

正确答案

解析

因为b≠0，所以b＝xe1＋ye2，x≠0，y≠0.

又|b|2＝(xe1＋ye2)2＝x2＋y2＋xy，，不妨设，则，当时，t2＋t＋1取得最小值，此时取得最大值，所以的最大值为2

知识点

平面向量的基本定理及其意义平面向量数量积的运算数量积表示两个向量的夹角

题型：单选题

单选题 · 5 分

已知向量，则下列能使成立的一组向量是 [答] （）。

正确答案

解析

略

知识点

平面向量的基本定理及其意义

题型：简答题

简答题 · 12 分

正确答案

见解析。

解析

（1）,

。

（2）因为,所以。

因为和共线,所以可设。

所以解得。

知识点

平面向量的基本定理及其意义向量在几何中的应用

题型：单选题

单选题 · 5 分

如图所示，点、、是圆上的三点，线段与线段交于圆内一点，若，则（）

正确答案

解析

略

知识点

平面向量的基本定理及其意义向量在几何中的应用与圆有关的比例线段

题型：填空题

填空题 · 4 分

平面直角坐标系中，O为原点，A、B、C三点满足，则= 。

正确答案

解析

略

知识点

向量的模平面向量的基本定理及其意义

题型：单选题

单选题 · 5 分

如图所示，是圆上的三个点，的延长线与线段交于圆内一点,若，则

正确答案

解析

略

知识点

向量的加法及其几何意义平面向量的基本定理及其意义向量在几何中的应用

题型：填空题

填空题 · 4 分

已知是夹角为的两个单位向量，向量若，则实数的值为

正确答案

解析

略

知识点

平面向量的基本定理及其意义平面向量共线（平行）的坐标表示

题型：填空题

填空题 · 5 分

在△中，分别为的中点，为上的点，且，若（），则（）。

正确答案

解析

略

知识点

平面向量的基本定理及其意义向量在几何中的应用

题型：单选题

单选题 · 5 分

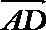
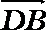
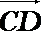
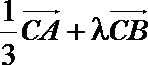
7.在∆ABC中，已知D是AB边上一点，若=2，=，则λ=（）

C-

D-

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面向量的基本定理及其意义向量在几何中的应用

继续学习学习下一知识点

下一知识点 : 平面向量的坐标运算

百度题库 > 高考 > 文科数学 > 平面向量的基本定理及其意义

扫码查看完整答案与解析