- 棱锥的结构特征
- 共18题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
如图,四棱锥S-ABCD中,SD


(1)证明:SE=2EB;
(2)求二面角A-DE-C的大小 。
正确答案
见解析。
解析
解法一:
(1)连接BD,取DC的中点G,连接BG,
由此知 


又
所以,
作
故
DE⊥平面SBC,DE⊥EC,DE⊥SB
所以,SE=2EB
(2)由

故
取


连接

所


连接AG,A



所以,二面角
解法二:
以D为坐标原点,射线


设A(1,0,0),则B(1,1,0),C(0,2,0),S(0,0,2)
(1)
设平面SBC的法向量为
由
故2b-2c=0,-a+b=0
令a=1,则b=c,c=1,
又设

设平面CDE的法向量
由

故 
令

由平面DEC⊥平面SBC得

故SE=2EB
(2)由(1)知

故
又


向量


于是
所以,二面角
知识点
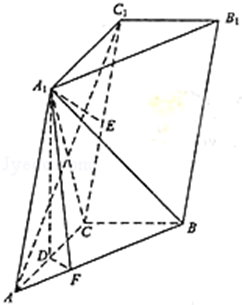
如图,三棱柱ABC﹣A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2。
(1)证明:AC1⊥A1B;
(2)设直线AA1与平面BCC1B1的距离为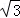
正确答案
见解析。
解析
(1)∵A1D⊥平面ABC,A1D⊂平面AA1C1C,
∴平面AA1C1C⊥平面ABC,又BC⊥AC
∴BC⊥平面AA1C1C,连结A1C,
由侧面AA1C1C为菱形可得AC1⊥A1C,
由三垂线定理可得AC1⊥A1B;
(2)∵BC⊥平面AA1C1C,BC⊂平面BCC1B1,
∴平面AA1C1C⊥平面BCC1B1,
作A1E⊥CC1,E为垂足,可得A1E⊥平面BCC1B1,
又直线AA1∥平面BCC1B1,
∴A1E为直线AA1与平面BCC1B1的距离,即A1E=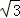
∵A1C为∠ACC1的平分线,∴A1D=A1E=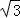
作DF⊥AB,F为垂足,连结A1F,
由三垂线定理可得A1F⊥AB,
∴∠A1FD为二面角A1﹣AB﹣C的平面角,
由AD=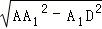
∴DF=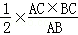
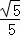
∴tan∠A1FD=
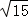
∴二面角A1﹣AB﹣C的大小为arctan
知识点
如题(21)图,设椭圆






(1)求该椭圆的标准方程;
(2)设圆心在

正确答案
(1)椭圆的标准方程为
(2)圆C的半径=
解析
(1)设F1(﹣c,0),F2(c,0),其中c2=a2﹣b2,
由



从而



从而|DF1|=




因此|DF2|=
所以2a=|DF1|+|DF2|=2

因此,所求椭圆的标准方程为
(2)设圆心在y轴上的圆C与椭圆
y1>0,y2>0,F1P1,F2P2是圆C的切线,且F1P1⊥F2P2,由圆和椭圆的对称性,易知x2=﹣x1,y1=y2,|P1P2|=2|x1|,
由(1)知F1(﹣1,0),F2(1,0),所以



由椭圆方程得1﹣



当x1=0时,P1,P2重合,此时题设要求的圆不存在;
当x1=﹣
由F1P1,F2P2是圆C的切线,且F1P1⊥F2P2,知CP1⊥CP2,又|CP1|=|CP2|,
故圆C的半径|CP1|=


知识点
已知数列






(1)求


(2) 设


(3) 设



正确答案
见解析
解析
(1)因为

又
当




当




当




(2) 对任意



②-③得 
④代入①得 
即 
又 
由⑤式,对所有


所以
(3) 解法1。由(2)可得 
于是,对任意




…………………

将以上各式相加,得

所以 
此式对
由④式

从而


所以对任意


对于
解法2。由(2)可得 
则 

所以


所以

以下同解法1。
知识点
扫码查看完整答案与解析