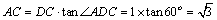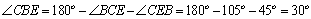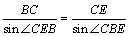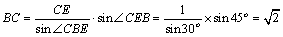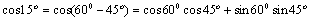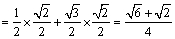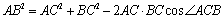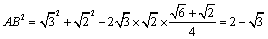- 平面的概念、画法及表示
- 共36题
正方体




正确答案
解析
略
知识点
在四边形ABCD中,


正确答案
解析
略
知识点
如图7,


(1)证明:四边形
(2)证明:
(3)求三棱锥
正确答案
见解析。
解析
(1)因为圆柱的上下底面平行,且FB、
所以FB//
依题意得,正六边形ABCDEF是圆内接正六边形,
所以,正六边形的边长等于圆的半径,即AB=AF=1.
在ABF中,由正六边形的性质可知,
所以,
同理可得

(2)
连结FC,则FC是圆柱上底面的圆的直径,∵
又∵B1B⊥平面ABCDEF,BF平面ABCDEF,∴BF⊥B1B
∵B1B∩BC=B,∴BF⊥平面B1BCC1.
又∵B1C平面B1BCC1,∴FB⊥CB1.
(3)连结F1C1,则四边形CFF1C1是矩形,且FC=F1C1=2,FF1⊥F1C1.
在RT FF1C1中,
∴三棱锥A1—ABF的体积
又三棱锥A1—ABF的体积等于三棱锥A—A1BF的体积,
∴三棱锥A—A1BF的体积等于
知识点
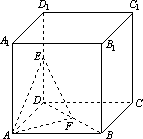
如图所示,在棱长为2的正方体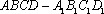
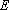
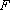
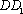
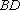
中点。
(1)求三棱锥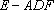
(2)求异面直线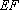
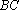
正确答案
(1)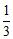
解析
(1)在正方体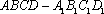
∵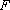
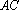
∴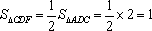
又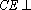
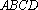
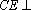

故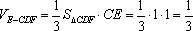
所以三棱锥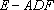

(2)连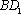
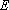
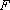
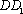
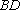
可得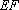
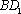
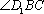
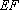
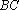
∵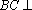
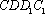
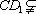
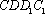
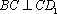
在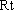
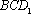
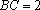
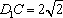
∴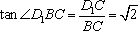
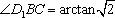
所以异面直线EF与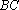
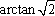
知识点
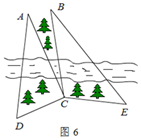
如图6,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据: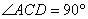
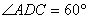

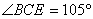
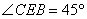
(1)求△CDE的面积;
(2)求A,B之间的距离.
正确答案
答案: 见解析。
解析
(1)连结DE,在CDE中,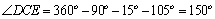
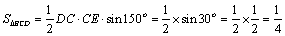
(2)依题意知,在RTACD中,
在BCE中,
由正弦定理
得
∵
在ABC中,由余弦定理
可得
∴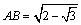
知识点
扫码查看完整答案与解析