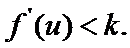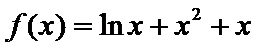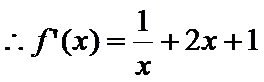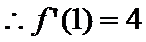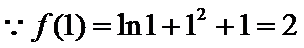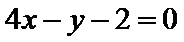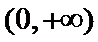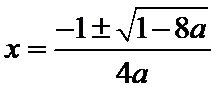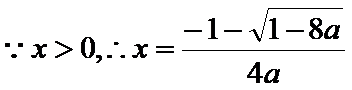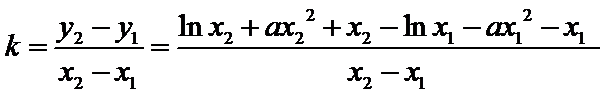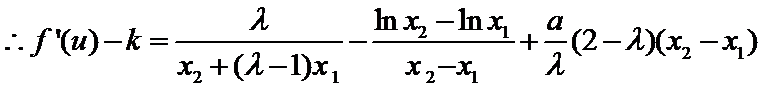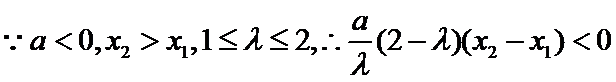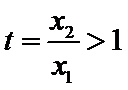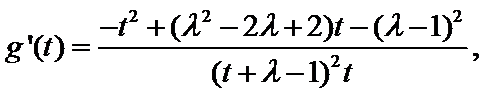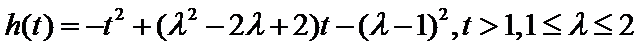- 函数的单调性及单调区间
- 共89题
12.已知函数





正确答案
解析


(1)当



(2)当













考查方向
解题思路
1.先求导后判断导数的正负,2.当导数有正有负时转化为一元二次方程根的分布处理,接着转化为线性规划使得问题得以解决。
易错点
1.不知道题中的条件:函数



知识点
已知函数



25.求函数
26.求证:
正确答案
(Ⅰ)

解析
解:(1)
令



令



考查方向
解题思路
在(Ⅱ)中要构造函数,通过求导研究单调性.
易错点
求单调性注意定义域;导数的运算.
正确答案
(Ⅱ)略.
解析


则
令
则


而



即

则





则


故

故
考查方向
解题思路
在(Ⅱ)中要构造函数,通过求导研究单调性.
易错点
求单调性注意定义域;导数的运算.
设函数
26.若


27.当

28.若


正确答案
(1)
解析
(Ⅰ)若


得
考查方向
解题思路
根据导数的几何意义求解,
易错点
不清楚
正确答案
(2)


解析
(Ⅱ)由
当

当


由表可知:


所以,当


考查方向
解题思路
先求导,然后判断单调性后即可得到单调区间;
易错点
不清楚
正确答案
(3)略
解析
(Ⅲ)当

令
由指数函数及幂函数的性质知:

又




设


由
当


当


所以当
又
考查方向
解题思路
先将要求的函数变形为
易错点
不会构造函数解决问题,当所要的函数正负不确定时,不知道应该设零点解决。
已知函数

20.若

21.若函数


正确答案



解析
解:
根据函数的图象可得, 


考查方向
解题思路
先将函数按照绝对值意义作分段函数,根据函数的图像,可求得单调区间
易错点
恰当选择a的分类标准,讨论区间
正确答案
解析
解:
(1).当





所以
在

(2).当



所以
综合(1)(2)得, 
考查方向
解题思路
结合函数的图象,对a进行分类
易错点
恰当选择a的分类标准,讨论区间
已知函数
27.若



28.求函数
29.设



正确答案

解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)利用导函数求出切线方程;(2)对



(Ⅰ)若



则曲线


而



……………3分
考查方向
解题思路
本题考查导数的性质及其几何意义的应用,解题步骤如下:求出原函数的导函数,确定切线斜率再求出切线方程。对



易错点
第二问在对
第三问在研究区间
正确答案
函数



函数

解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)利用导函数求出切线方程;(2)对



(Ⅱ)函数


(1)当



令



令


所以当


所以函数


单调增区间为

(2)当



当



当




即当



(3)当

令







令


所以函数



函数

考查方向
解题思路
本题考查导数的性质及其几何意义的应用,解题步骤如下:求出原函数的导函数,确定切线斜率再求出切线方程。对



易错点
第二问在对
第三问在研究区间
正确答案
当


解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)利用导函数求出切线方程;(2)对



(Ⅲ)(1)当


所以不存在极值点;
(2)当


在
若函数


解得

所以
综上所述,当


…………13分
考查方向
解题思路
本题考查导数的性质及其几何意义的应用,解题步骤如下:求出原函数的导函数,确定切线斜率再求出切线方程。对



易错点
第二问在对
第三问在研究区间
已知函数f(x)=x3+ax2+b(a,b∈R).
25.试讨论f(x)的单调性;
26.若b=c﹣a(实数c是与a无关的常数),当函数f(x)有三个不同的零点时,a的取值范围恰好是(﹣∞,﹣3)∪(1,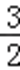
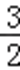
正确答案
函数f(x)在(﹣∞,0),(﹣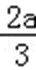
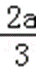
解析
(1)∵f(x)=x3+ax2+b,
∴f′(x)=3x2+2ax,
令f′(x)=0,可得x=0或﹣
a=0时,f′(x)>0,∴f(x)在(﹣∞,+∞)上单调递增;
a>0时,x∈(﹣∞,﹣

∴函数f(x)在(﹣∞,﹣
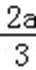
a<0时,x∈(﹣∞,0)∪(﹣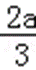
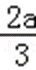
∴函数f(x)在(﹣∞,0),(﹣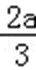
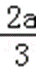
考查方向
解题思路
(1)求导数,分类讨论,利用导数的正负,即可得出f(x)的单调性;
易错点
本题考查导数知识的综合运用,考查函数的单调性,分类讨论中易错
正确答案
c=1
解析
(2)由(1)知,函数f(x)的两个极值为f(0)=b,f(﹣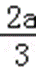
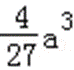
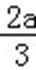
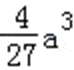
∵b=c﹣a,
∴a>0时,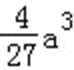
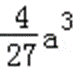
设g(a)=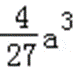
∵函数f(x)有三个不同的零点时,a的取值范围恰好是(﹣∞,﹣3)∪(1,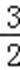
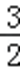
∴在(﹣∞,﹣3)上,g(a)<0且在(1,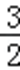
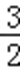
∴g(﹣3)=c﹣1≤0,且g(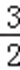
∴c=1,
此时f(x)=x3+ax2+1﹣a=(x+1)[x2+(a﹣1)x+1﹣a],
∵函数有三个零点,
∴x2+(a﹣1)x+1﹣a=0有两个异于﹣1的不等实根,
∴△=(a﹣1)2﹣4(1﹣a)>0,且(﹣1)2﹣(a﹣1)+1﹣a≠0,
解得a∈(﹣∞,﹣3)∪(1,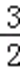
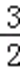
综上c=1.
考查方向
解题思路
(2)由(1)知,函数f(x)的两个极值为f(0)=b,f(﹣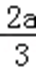
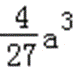
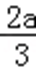
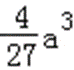
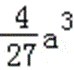
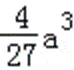
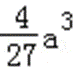
易错点
本题考查导数知识的综合运用,考查函数的单调性,考查函数的零点,在用范围的过程中易错.
已知函数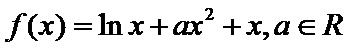
25.当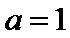
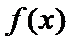
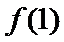
26.讨论函数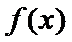
27.已知
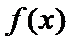
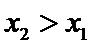

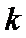
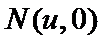
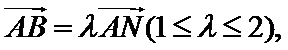
正确答案
详见解析
解析
(Ⅰ)当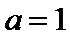
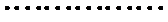
又

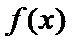


即
考查方向
导数的几何意义和切线方程
解题思路
先求导,代入a=1,然后求出切线的方程
易错点
计算能力弱,求导错误
正确答案
详见解析
解析
(Ⅱ)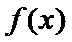
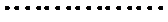
当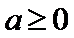
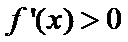
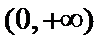
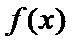
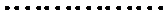
当

则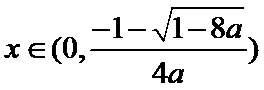
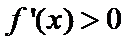
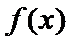
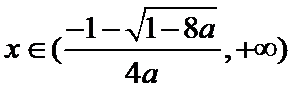
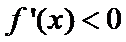
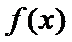
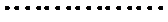
综上,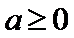


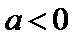
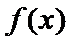
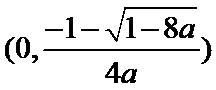


考查方向
导数和函数的综合题
利用导数求函数的单调性和单调区间
解题思路
先求定义域,然后在其定义域内判断函数的单调性,并求出单调区间
易错点
分类讨论有重复和遗漏
正确答案
详见解析
解析
(Ⅲ)证明:
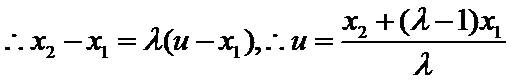
又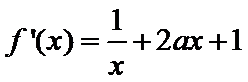
要证: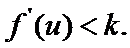
即证: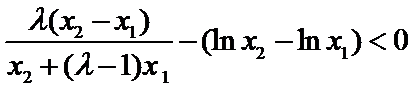
令
令
对称轴
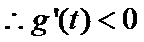
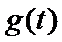
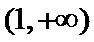
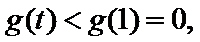

…….12分
考查方向
利用导数证明不等式
构造函数,利用函数的单调性证明不等式
导数、函数、不等式的综合应用
解题思路
先求导,然后根据不等式性质,够造出恰当的函数,然后令其导函数小于K
易错点
构造函数错误,计算能力弱
某歌星租用大华体育馆举办个人演唱会,每场租金30000元,共演出三场,由体育馆售票,共取得票款收入600000元,按票款收入的2%向歌星经纪人支付佣金。营业税税率为3%。体育馆应为该歌星代扣代缴的营业税税额为( )元。
A.15300
B.14940
C.18000
D.17640
正确答案
B
解析
(600000-30000×3-600000X2%)×39%=14940(元)
根据《中华人民共和国广告法》,不得发布广告的药品为
A.人血白蛋白
B.氨茶碱
C.可待图片
D.狂犬疫苗
E.龙胆泻肝九
正确答案
C
解析
禁止发布广告的药品包括:麻醉药品、精神药品、医疗用毒性药品、放射性药品。可待因片属于麻醉药品,故选C。
扫码查看完整答案与解析