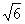- 平面向量数量积的坐标表示、模、夹角
- 共10题
3.已知向量


正确答案
知识点
5.设


①若

②若

③若


④若

其中真命
正确答案
解析
第1个,两直线也可能为异面直线,故错误,第2个正确,第三个也可能是m在平面呢,故错误,第4个比如正方体的相邻的三个面,就是反例,所以真命题只有1个,所以选B
考查方向
解题思路
根据直线与平面的位置关系的特征,逐一判断
易错点
考虑直线和平面位置关系考虑不周全
知识点
6.若非零向量a,b满足|a|=

正确答案
解析
由题意




考查方向
解题思路
本题考查两向量的夹角,涉及到向量的模,向量的垂直,向量的数量积等知识,体现了数学问题的综合性,考查学生运算求解能力,综合运用能力.
易错点
向量数量积运算的化简
知识点
15.在实数集R中,我们定义的大小关系“>”为全体实数排了一个“序”.类似的,我们在平面向量集






①若

②若

③若

④对于任意向量


其中真命题的序号为
正确答案
①②③
解析
解析已在路上飞奔,马上就到!
知识点
8.已知向量












正确答案
解析
根据题意可知,
由
可得
所以
考查方向
向量的线性运算与向量的数量积
解题思路
根据题意先表示出向量夹角的坐标形式,然后求解
易错点
对向量的数量积性质掌握不牢
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
平面直角坐标系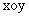
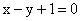
(1)求圆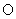
(2)若直线
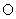
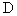
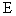
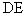
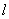
(3)设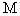
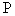
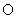
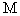
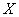
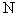
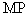
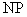
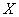
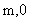
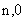
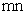
正确答案
见解析。
解析
(1)因为
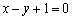
所以圆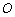
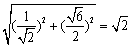
故圆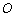
(2)设直线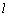
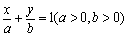
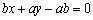
由直线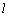
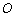
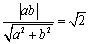
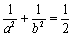
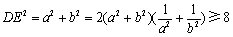
当且仅当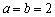
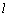
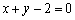
(3)设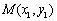
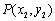
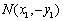
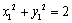
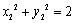
直线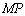
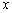
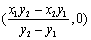
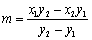
直线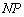
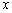
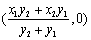
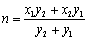
故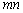
知识点
正项数列

(1)求数列

(2)令



正确答案
见解析
解析
解:(1)由已知可得:
(2)
所以
知识点
设函数


(1)求

(2)求函数
正确答案
见解析
解析
(1)







又



当且仅当



(2)由

得





知识点
5.已知向量
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析